Intervalos de confianza
Taller intervalos de confianza
Definiciones
| Nivel de confianza NC | Nivel de significancia \(\alpha\). |
|---|---|
| Probabilidad máxima con la que podríamos asegurar que el parámetro a estimar se encuentra dentro de nuestro intervalo estimado | Es la probabilidad máxima que asumimos de forma voluntaria de equivocarnos al rechazar la hipótesis nula cuando en realidad es cierta |
| Representa el porcentaje de intervalos que tomados de 100 muestras independientes distintas contienen en realidad el valor desconocido. | Máximo error que se comete en la estimación |
\[\Large NC+\alpha=1\] Si se construyen 100 intervalos de la forma \(\hat \theta_{inf}<\theta<\hat \theta_{sup}\) con un NC=0.97 entonces se espera que 97 de los 100 intervalos contengan el parámetro \(\theta\)

Nivel de confianza y de significancia

\[\Huge NC+\alpha=100\% \]
| NC | NS \(\alpha\) | \(Z_\alpha\) | \(\alpha/2\) | \(Z_{\alpha/2}\) |
|---|---|---|---|---|
| 90% | 10% | 5% | ||
| 95% | 5% | 2.5% | ||
| 99% | 1% | 0.05% |
Estimación por intervalo
Una estimación por intervalo de un parámetro \(\theta\) de la población es un intervalo de la forma:
\[\Large \hat \theta_{inf}<\theta<\hat \theta_{sup}\] Donde los valores estimados dependen del valor estimado de \(\theta\) y de la distribución de muestreo.
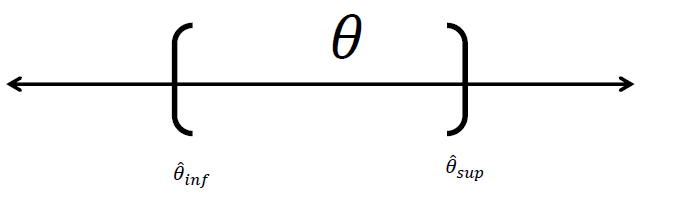
Intervalo de confianza para una muestra
IC para la media
## Warning: package 'DiagrammeR' was built under R version 4.5.2con la varianza conocida
Si \(\bar x\) es la media de una muestra aleatoria de tamaño 𝑛 de una población normal con varianza \(\sigma^2\) conocida, un intervalo de confianza del 1 − 𝛼 100% para 𝜇 está dado por:
\[\Large \bar x-Z_{\alpha/2} \frac{\sigma}{\sqrt n} \leq \mu \leq \bar x+Z_{\alpha/2} \frac{\sigma}{\sqrt n}\]
donde \(Z_{\alpha/2}\) es el valor z que deja un área de 𝛼/2 a la derecha.
Ejemplo Una muestra aleatoria de 110 relámpagos dieron por resultado una duración de eco de radar promedio muestral de 0.81 segundos y una desviación estándar de 0.34 segundos. Calcule un intervalo de confianza de 95% para la duración de eco promedio e interprete el intervalo resultante
library(BSDA)## Warning: package 'BSDA' was built under R version 4.5.2## Cargando paquete requerido: lattice##
## Adjuntando el paquete: 'BSDA'## The following object is masked from 'package:datasets':
##
## Orangezsum.test(mean.x=0.81,sigma.x=0.34, n.x=110,conf.level=0.95)##
## One-sample z-Test
##
## data: Summarized x
## z = 24.986, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 0.7464624 0.8735376
## sample estimates:
## mean of x
## 0.81Intervalo de confianza para la media con varianza conocida
con la varianza desconocida
Si \(\bar x\) es la media de una muestra aleatoria de tamaño 𝑛 de una población normal con varianza \(\sigma^2\) desconocida, un intervalo de confianza del 1 − 𝛼 100% para 𝜇 está dado por:
\[\Large \bar x-t_{\alpha/2} \frac{s}{\sqrt n} \leq \mu \leq \bar x+t_{\alpha/2} \frac{s}{\sqrt n}\]
donde \(Z_{\alpha/2}\) es el valor z que deja un área de 𝛼/2 a la derecha.
Ejemplo Se tienen los datos de las horas de ejercicio que hacen 10 adolescentes por semana, calcule un intervalo de confianza para el tiempo promedio con un NC del 90%
library(carData)##
## Adjuntando el paquete: 'carData'## The following objects are masked from 'package:BSDA':
##
## Vocab, WoolcarData::Blackmore$exercise[1:10]## [1] 2.71 1.94 2.36 1.54 8.63 0.14 0.14 0.00 0.00 5.08x=carData::Blackmore$exercise[1:10]
t.test(x=x,conf.level = 0.9)##
## One Sample t-test
##
## data: x
## t = 2.5824, df = 9, p-value = 0.02958
## alternative hypothesis: true mean is not equal to 0
## 90 percent confidence interval:
## 0.6539884 3.8540116
## sample estimates:
## mean of x
## 2.254Intervalo de confianza para la media con varianza desconocida
IC para la proporción
Si \(\hat p\) es la proporción de éxitos en una muestra aleatoria de tamaño 𝑛, un intervalo de confianza aproximado de (1−𝛼) 100% para 𝑝 está dado por
\[\Large \hat p-Z_{\alpha/2} \sqrt{\frac{\hat p(1-\hat p)}{n}}\leq p \leq \hat p+Z_{\alpha/2} \sqrt{\frac{\hat p(1-\hat p)}{n}} \]
donde \(𝑍_{𝛼/2}\) es el valor z que deja un área de 𝛼/2 a la derecha. Nota: usar solo cuando 𝑛𝑝≥50 y 𝑛(1 −𝑝)≥50
EJEMPLO Se seleccionó una muestra de 487 mujeres no fumadoras de peso normal (que había dado a luz). 7.2% de estos nacimientos dieron por resultado niños con bajo peso al nacer (menos de 2500 g). Calcule un intervalo de confianza con un nivel de confianza del 93% para la proporción de todos esos nacimientos que dieron por resultado niños de bajo peso al nacer.
prop.test(x=72,n=1000,conf.level=0.93)##
## 1-sample proportions test with continuity correction
##
## data: 72 out of 1000, null probability 0.5
## X-squared = 731.02, df = 1, p-value < 2.2e-16
## alternative hypothesis: true p is not equal to 0.5
## 93 percent confidence interval:
## 0.05809659 0.08879847
## sample estimates:
## p
## 0.072Intervalo de confianza para la proporción
IC para la varianza
Si \(𝑠^2\) es la varianza de una muestra aleatoria de tamaño 𝑛 de una población normal, un intervalo de confianza aproximado de (1−𝛼) 100% para \(𝜎^2\) está dado por
\[\Large \frac {(n−1)𝑠^2}{\chi^2_{ \frac {𝛼} {2},𝑛−1} } <𝜎^2<\frac {(n−1)𝑠^2}{\chi^2_{1- \frac {𝛼} {2},𝑛−1} }\]
donde los denominadores son obtenidos de una chi-cuadrada. Nota: un intervalo de confianza para 𝜎 se puede obtener tomando raíz cuadrada en los límites del intervalo anterior.
Ejemplo
Se tienen los datos de las horas de ejercicio que hacen 10 adolescentes por semana, calcule un intervalo de confianza para la varianza del tiempo con un NC del 98%.
library(EnvStats)## Warning: package 'EnvStats' was built under R version 4.5.2##
## Adjuntando el paquete: 'EnvStats'## The following objects are masked from 'package:stats':
##
## predict, predict.lm## The following object is masked from 'package:base':
##
## print.defaultlibrary(carData)
carData::Blackmore$exercise[1:10]## [1] 2.71 1.94 2.36 1.54 8.63 0.14 0.14 0.00 0.00 5.08x=carData::Blackmore$exercise[1:10]
varTest(x, conf.level=0.95)## $statistic
## Chi-Squared
## 68.56624
##
## $parameters
## df
## 9
##
## $p.value
## [1] 5.813905e-11
##
## $estimate
## variance
## 7.618471
##
## $null.value
## variance
## 1
##
## $alternative
## [1] "two.sided"
##
## $method
## [1] "Chi-Squared Test on Variance"
##
## $data.name
## [1] "x"
##
## $conf.int
## LCL UCL
## 3.60443 25.39124
## attr(,"conf.level")
## [1] 0.95
##
## attr(,"class")
## [1] "htestEnvStats"Intervalo de confianza para la varianza
Intervalos de confianza para dos muestras
IC para la diferencia de medias
Si el intervalo contiene el cero significa que hay igualdad entre medias
Con varianzas conocidas
Si\(\bar x_1\) y \(\bar x_2\)son las medias muestrales aleatorias independientes de tamaño \(n_1\) y \(n_2\) de poblaciones normales con varianzas conocidas \(\sigma_1\) y \(\sigma_2\) respectivamente, un intervalo de confianza de 1-𝛼 100 para \(\mu_1-\mu_2\) está dado por:
\[\Large (\bar x_1-\bar x_2)-Z_{\frac{\alpha}{2}}\sqrt{\left( \frac{\sigma_1^2}{n_1}\right)+\left( \frac{\sigma_2^2}{n_2}\right)}<\mu_1-\mu_2< (\bar x_1-\bar x_2)+Z_{\frac{\alpha}{2}}\sqrt{\left( \frac{\sigma_1^2}{n_1}\right)+\left( \frac{\sigma_2^2}{n_2}\right)}\]
Con varianzas desconocidas pero iguales
Si\(\bar x_1\) y \(\bar x_2\)son las medias muestrales aleatorias independientes de tamaño \(n_1\) y \(n_2\) de poblaciones normales con varianzas iguales pero desconocidas $_1\(2𝑦\)_2$ respectivamente, un intervalo de confianza de (1-𝛼)100% para \(\mu_1-\mu_2\) está dado por:
\[\Large (\bar x_1-\bar x_2)-t_{\frac{\alpha}{2},v}S_p\sqrt{\left( \frac{1}{n_1}\right)+\left( \frac{1}{n_2} \right)}<\mu_1-\mu_2< (\bar x_1-\bar x_2)+ t_{\frac{\alpha}{2},v}S_p\sqrt{\left( \frac{1}{n_1}\right)+\left( \frac{1}{n_2}\right)}\] \[v=n_1-n_2-2\]
\[S^2_p=\frac{(n_1)S_1^2+(n_2)S_2^2}{n_1+n_2-2}\]
Intervalo de confianza para la diferencia de medias con varianzas iguales
Con varianzas desconocidas y diferentes
Si\(\bar x_1\) y \(\bar x_2\)son las medias muestrales aleatorias independientes de tamaño \(n_1\) y \(n_2\) de poblaciones normales con varianzas iguales pero desconocidas $_1\(2𝑦\)_2$ respectivamente, un intervalo de confianza de (1-𝛼)100% para \(\mu_1-\mu_2\) está dado por:
\[\Large (\bar x_1-\bar x_2)-t_{\frac{\alpha}{2},v}\sqrt{\left( \frac{S_1^2}{n_1}\right)+\left( \frac{S_2^2}{n_2} \right)}<\mu_1-\mu_2< (\bar x_1-\bar x_2)+ t_{\frac{\alpha}{2},v}\sqrt{\left( \frac{S_1^2}{n_1}\right)+\left( \frac{S_2^2}{n_2} \right)}\] \[v=\frac{\left( \left( \frac{S_1^2}{n_1}\right)+\left( \frac{S_2^2}{n_2} \right) \right) ^2}{\frac{\left( \frac{S_1^2}{n_1}\right)^2}{n_1-1}+\frac{\left( \frac{S_1^2}{n_1}\right)^2}{n_2-1}}\]
Intervalo de confianza para la diferencia de medias con varianzas desconocidas y diferentes
IC para la razón de varianzas
Entre los diferentes usos que se le da a este intervalo de confianza el principal consiste en determinar si hay igualdad entre dos varianzas, esto se afirma si el intervalo contiene al 1, de contenerlo se dice que hay evidencia de que las varianzas poblacionales son iguales.
\[\Large \frac{S_1^2}{S_2^2}f_{\frac{\alpha}{2},n_2-1,n_1-1}<\frac{\sigma_1^2}{\sigma_2^2}<\frac{S_1^2}{S_2^2}*f_{1-\frac{\alpha}{2},n_2-1,n_1-1}\]
Intervalo de confianza para la razón de varianzas
EJEMPLO
Se realizó una prueba para comparar un método nuevo con el método estándar. Se entrenaron dos grupos de 9 nuevos empleados cada grupo durante un período de un mes; Se midió el tiempo en minutos que necesito cada empleado en armar cierto dispositivo al final del período de entrenamiento; los resultados obtenidos fueron:
E<-c(32,37,35,28,41,44,35,31,34)
N<-c(35,31,29,25,34,40,27,32,31)Admitiendo que el tiempo de armado utilizado en ambos métodos son variables aleatorias independientes y distribuidas normalmente:
- ¿Tiene igual varianza?
###prueba de varianza
var.test(E,N)##
## F test to compare two variances
##
## data: E and N
## F = 1.2205, num df = 8, denom df = 8, p-value = 0.7849
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.2753114 5.4109136
## sample estimates:
## ratio of variances
## 1.220527¿Se puede aceptar la hipótesis de igualdad de tiempos de armado, en función de los datos y con un nivel de confianza del 95%?
t.test (E,N,paired=T,conf.level=0.95)##
## Paired t-test
##
## data: E and N
## t = 2.9938, df = 8, p-value = 0.01723
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
## 0.8423999 6.4909334
## sample estimates:
## mean difference
## 3.666667IC para la diferencia de proporciones
\(\bar p_x\) y \(\bar p_y\)son las proporciones de éxito de dos muestras aleatorias independientes de tamaño \(n_1\) y \(n_2\), entonces un intervalo de confianza de (1 −𝛼) 100% para \(𝑝1−𝑝2\) está dado por:
\[\Large (\bar p_x-\bar p_y)-Z_{\frac{\alpha}{2}}\sqrt{\frac{p_x q_x}{n_x}+ \frac{p_y q_y}{n_y}}<p_x-p_y<(\bar p_x-\bar p_y)+Z_{\frac{\alpha}{2}}\sqrt{\frac{p_x q_x}{n_x}+ \frac{p_y q_y}{n_y}}\] Si el intervalo contiene el cero significa que hay igualdad entre medias
Intervalo de confianza para la diferencia de proporciones
Ejemplo Dos grupos son considerados en un grupo sobre la efectividad de una nueva vacuna. El primer grupo, que recibe la vacuna contiene 200.745 individuos. El Segundo grupo, que recibe un placebo consiste de 201.229 individuos. Hubo 57 casos de enfermedad en el primer grupo y 142 casos en el segundo grupo. se desea saber si la vacuna es o no eficiente, use un intervalo de confianza con un nivel de significancia \(\alpha=0.05\) para conocer las relaciones entre las proporciones p1 y p2.
x <- c(57,142)
n <- c(200745,201229)
prop.test(x, n)##
## 2-sample test for equality of proportions with continuity correction
##
## data: x out of n
## X-squared = 35.273, df = 1, p-value = 2.866e-09
## alternative hypothesis: two.sided
## 95 percent confidence interval:
## -0.0005641508 -0.0002792920
## sample estimates:
## prop 1 prop 2
## 0.0002839423 0.0007056637Halle un intervalo de confianza al 95% para la diferencia de proporciones. Que concluye
Intervalo de confianza para la diferencia de medias pareadas
Si \(\hat d\) y \(𝑠_𝑑\) son la media y la desviación estándar de las diferencias distribuidas normalmente de 𝑛pares aleatorios de mediciones, entonces un intervalo de confianza de (1-𝛼)100% para \(𝜇_𝑑=𝜇_1-𝜇_2\) está dado por:
\[\Large \bar d-t_{\alpha/2} \frac{s}{\sqrt n} \leq \mu \leq \bar d+t_{\alpha/2} \frac{s}{\sqrt n}\] Ejemplo Se tienen los datos del coeficiente intelectual verbal y matemático de un grupo de personas, se desea saber si hay diferencias entre los coeficientes, use un intervalo de confianza para la diferencia pareada del 92%
#IQ MATEMATICO
iqm=carData::Wong$piq[1:10]
#IQ VERBAL
iq=carData::Wong$viq[1:10]
t.test(x=iqm,y=iq, paired = TRUE,conf.level = 0.92)##
## Paired t-test
##
## data: iqm and iq
## t = -0.82575, df = 9, p-value = 0.4303
## alternative hypothesis: true mean difference is not equal to 0
## 92 percent confidence interval:
## -10.844577 4.444577
## sample estimates:
## mean difference
## -3.2Intervalo de confianza para la diferencia de medias pareadas