Distribución normal
Distribución normal
Una distribución ampliamente usada y la más importante de toda la estadística, diversas poblaciones y fenómenos numéricos son representados por esta distribución por ejemplo
Errores de medición en experimentos científicos
Mediciones antropométricas
Tiempos de reacción en experimentos psicológicos
Mediciones de inteligencia y aptitud
Función de distribución de probabilidad
Esta distribución depende de los parámetros de localización y escala, determinados por la media \(E(X)=\mu\) y la desviación estándar \(sd = \sigma\),
El valor de \(\sigma\) es la distancia desde \(\mu\) hasta los puntos de inflexión de la curva (los puntos donde la curva cambia de concavidad de hacia abajo a hacia arriba).
La función de distribución de probabilidad está dada por:
\[\LARGE f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \] Con \(-\infty<\mu<\infty\) y \(\sigma>0\)
Si una variable se distribuye normal se denota de la forma:
\[\LARGE x \sim N(\mu, \sigma^2)\]
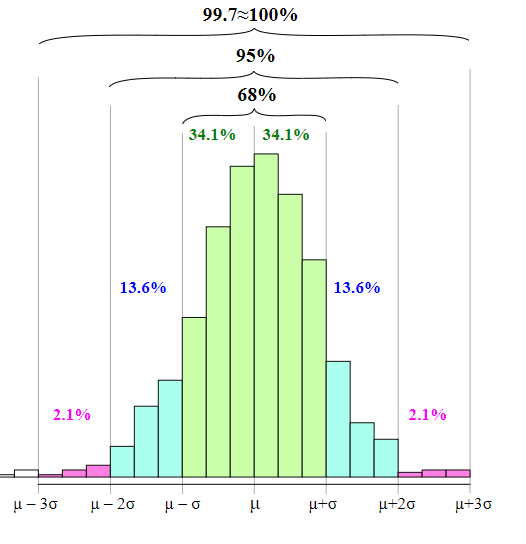
Si la distribución de la población de una variable es (aproximadamente) normal, entonces
- Aproximadamente 68% de los valores están dentro de 1 DE (desviación estándar) de la media.
\[\LARGE P(\mu-\sigma\leq x \leq \mu+\sigma)=68.27\%\]
Aproximadamente 95% de los valores están dentro de 2 DE de la media. \[\LARGE P(\mu-2\sigma\leq x \leq \mu+2\sigma)=95.45\%\]
Aproximadamente 99.7% de los valores están dentro de 3 DE de la media.
\[\LARGE P(\mu-3\sigma\leq x \leq \mu+3\sigma)=99.73\%\]
Aplicativo de distribuciones de probabilidad continuas
Distribución normal estándar
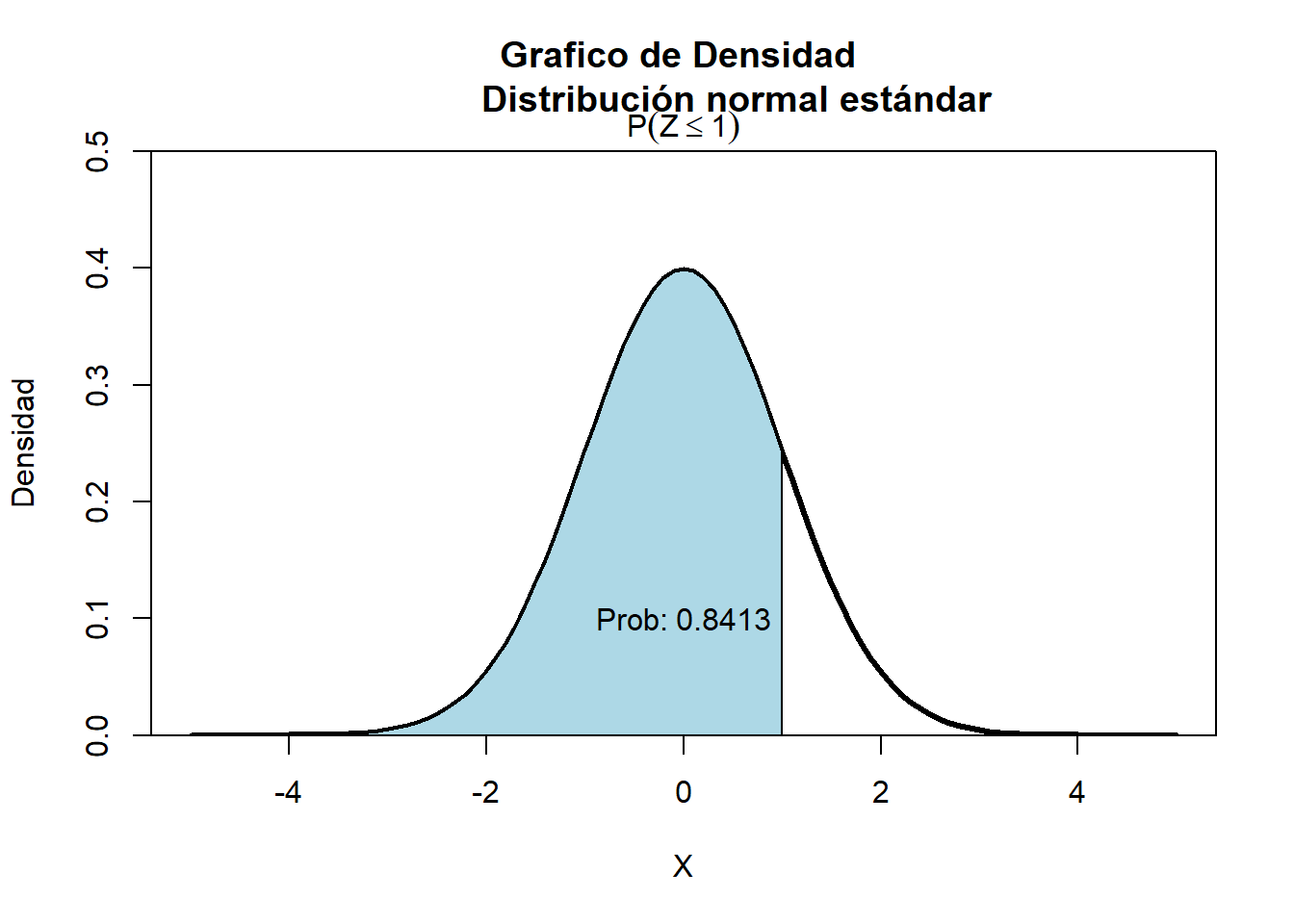
Una variable aleatoria normal con \(\mu=0\) y \(\sigma=1\), es llamada una variable aleatoria normal estándar y se denota como z.
\[\LARGE Z \sim N(0,1)\] ### Función de distribución de probabilidad acumulada
\[\LARGE \Phi(x)=P(Z \leq x)=F(x)\]
¿Cómo estandarizar una variable aleatoria?
Suponga x es una variable aleatoria normal con media \(\mu\) y varianza \(\sigma^2\), para estandarizar la variable se debe usar la formula:
\[\LARGE z=\frac{x-\mu}{\sigma}\]
Cualquier distribución Normal se puede convertir a una distribución Normal Estándar
Ejemplo 1
Se desea estandarizar una variable aleatoria con valor x=5.9, media \(\mu=5\) y desviación estándar \(sd=3\).
\[\LARGE z=\frac{5.9-5}{3}=?\]
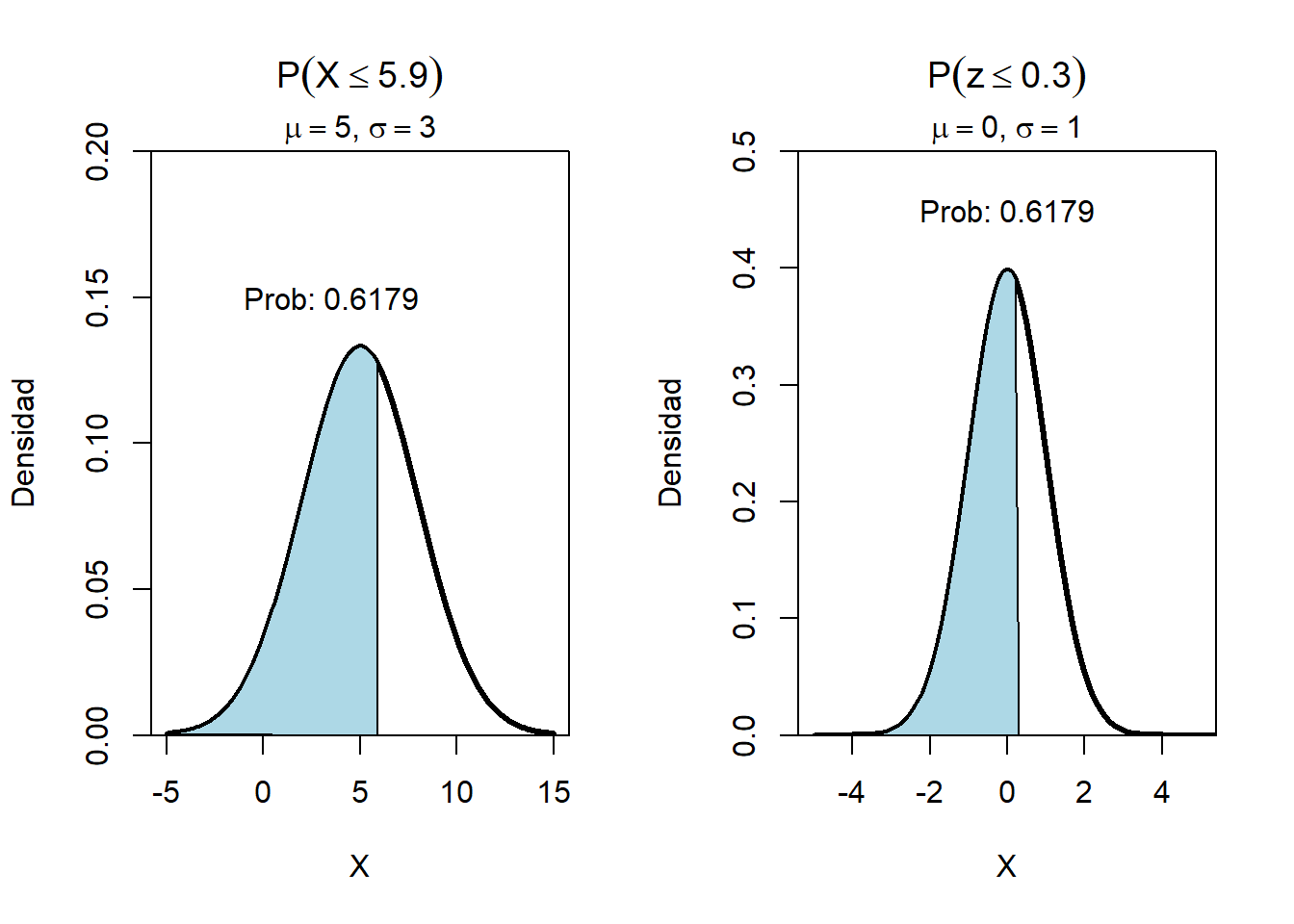
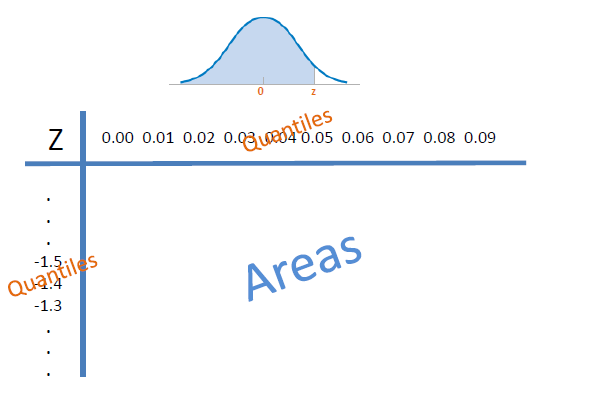
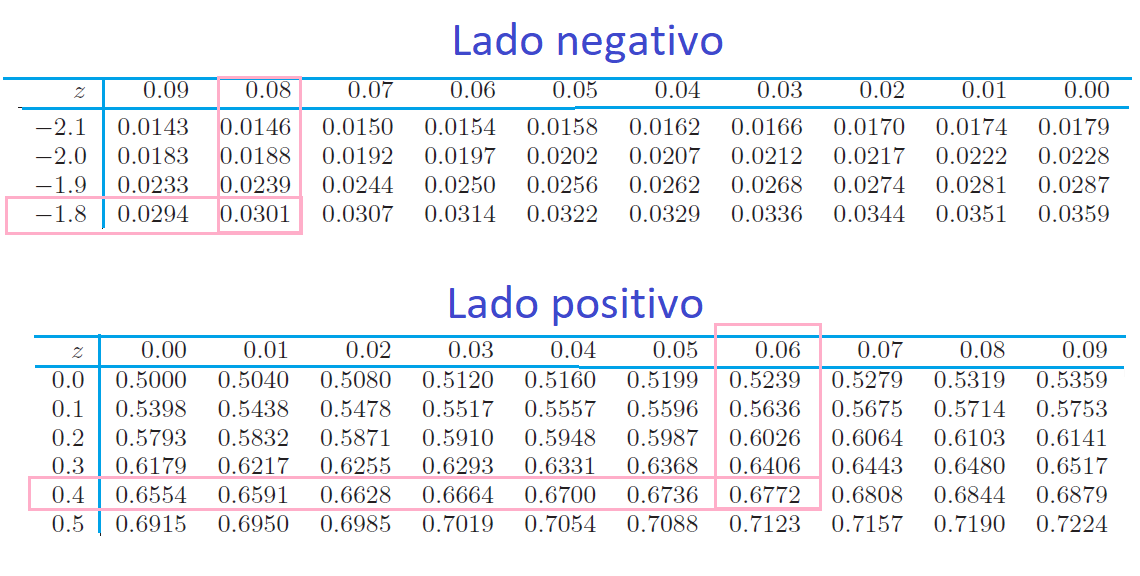
Tabla de la distribución normal
Estructura de la normal
Ejemplo 2
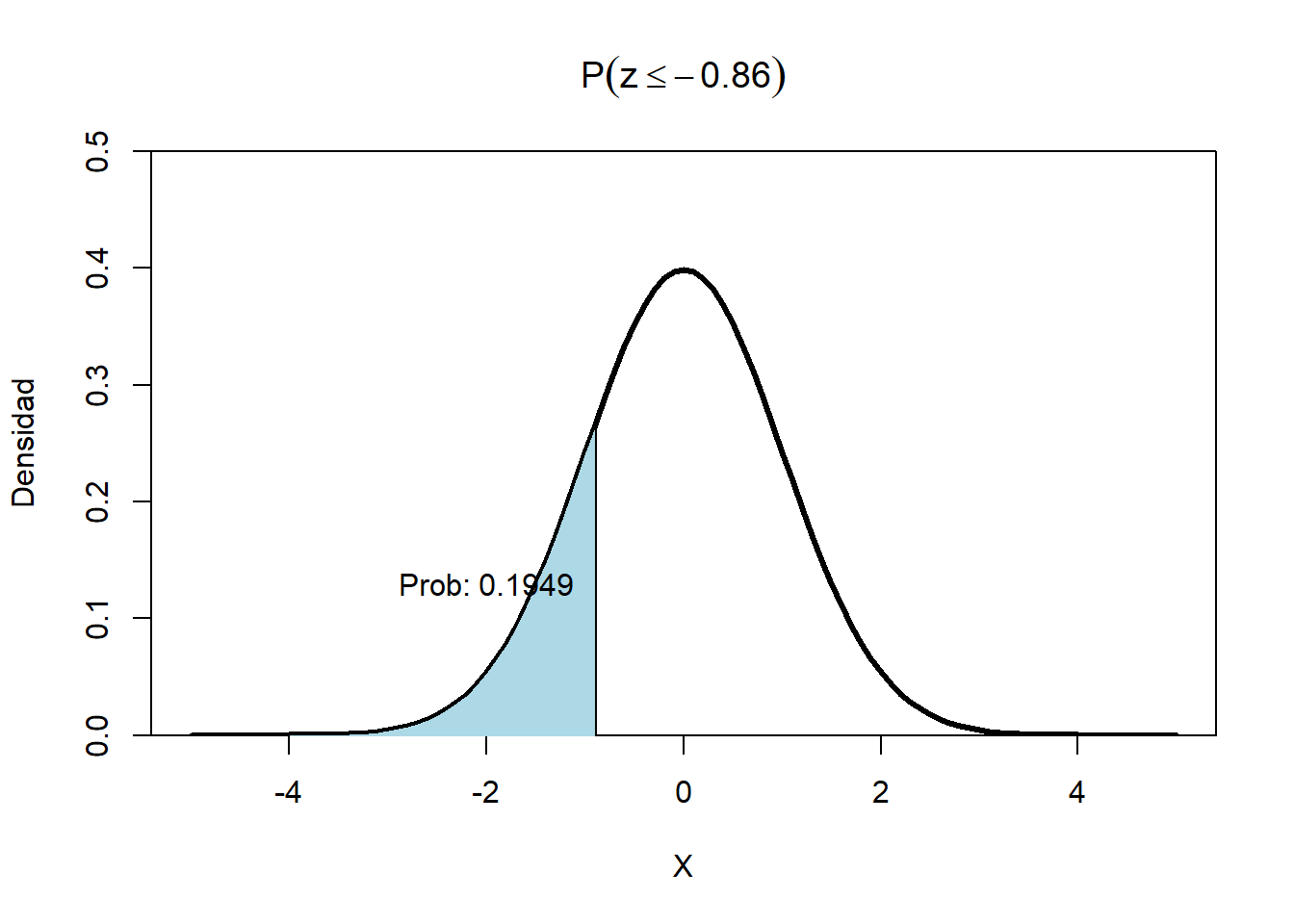
En la tabla buscar en el lado negativo: \[P(Z\leq -0.86)=0.1949\]
Ejemplo 3
\[P(Z\leq 1.37)=0.9147\]
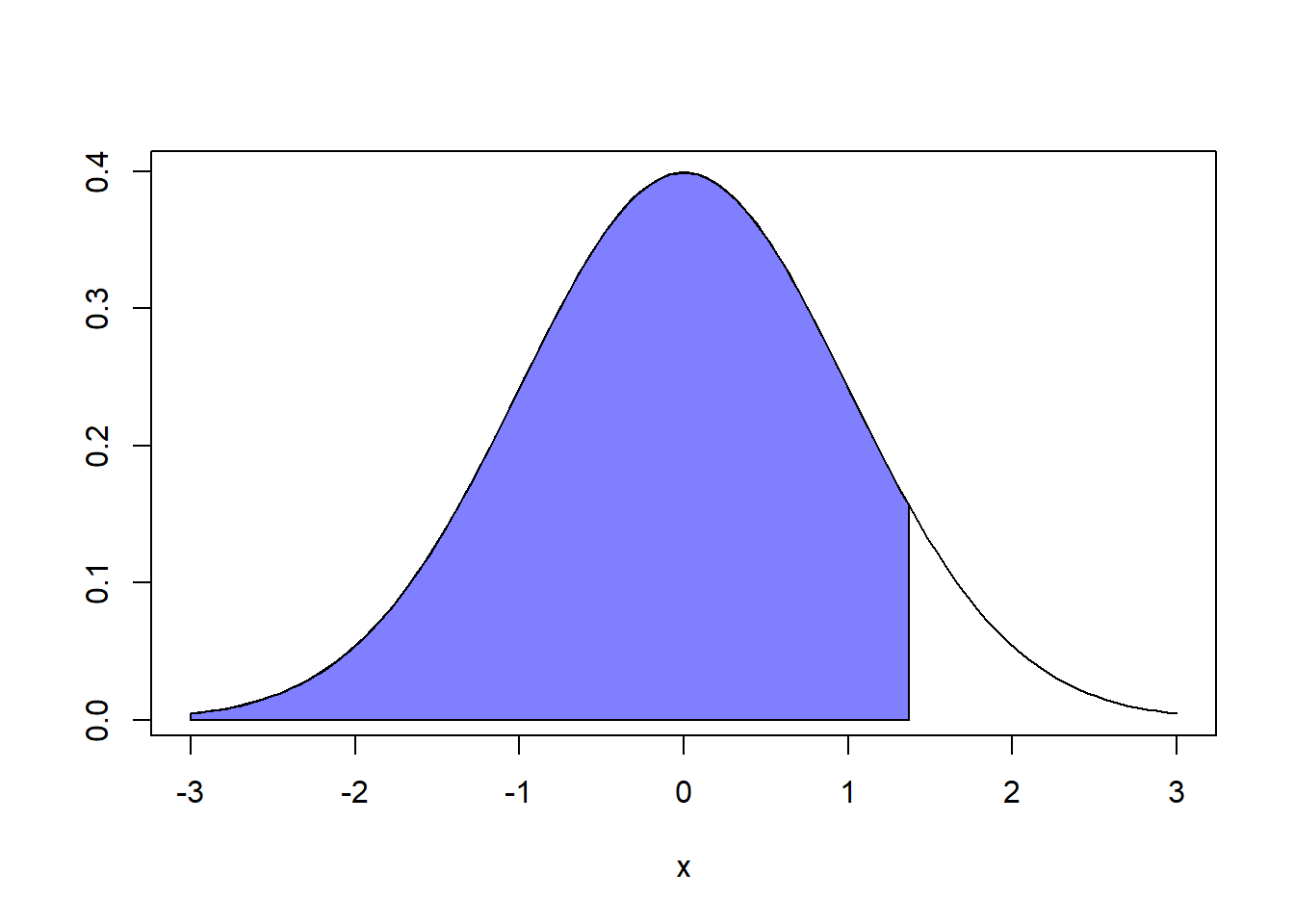
En la tabla buscar en el lado positivo: \[P(Z\leq 1.37)=0.9147\]
Ejemplo 4 \[P(-1.25\leq Z\leq 0.37)\]
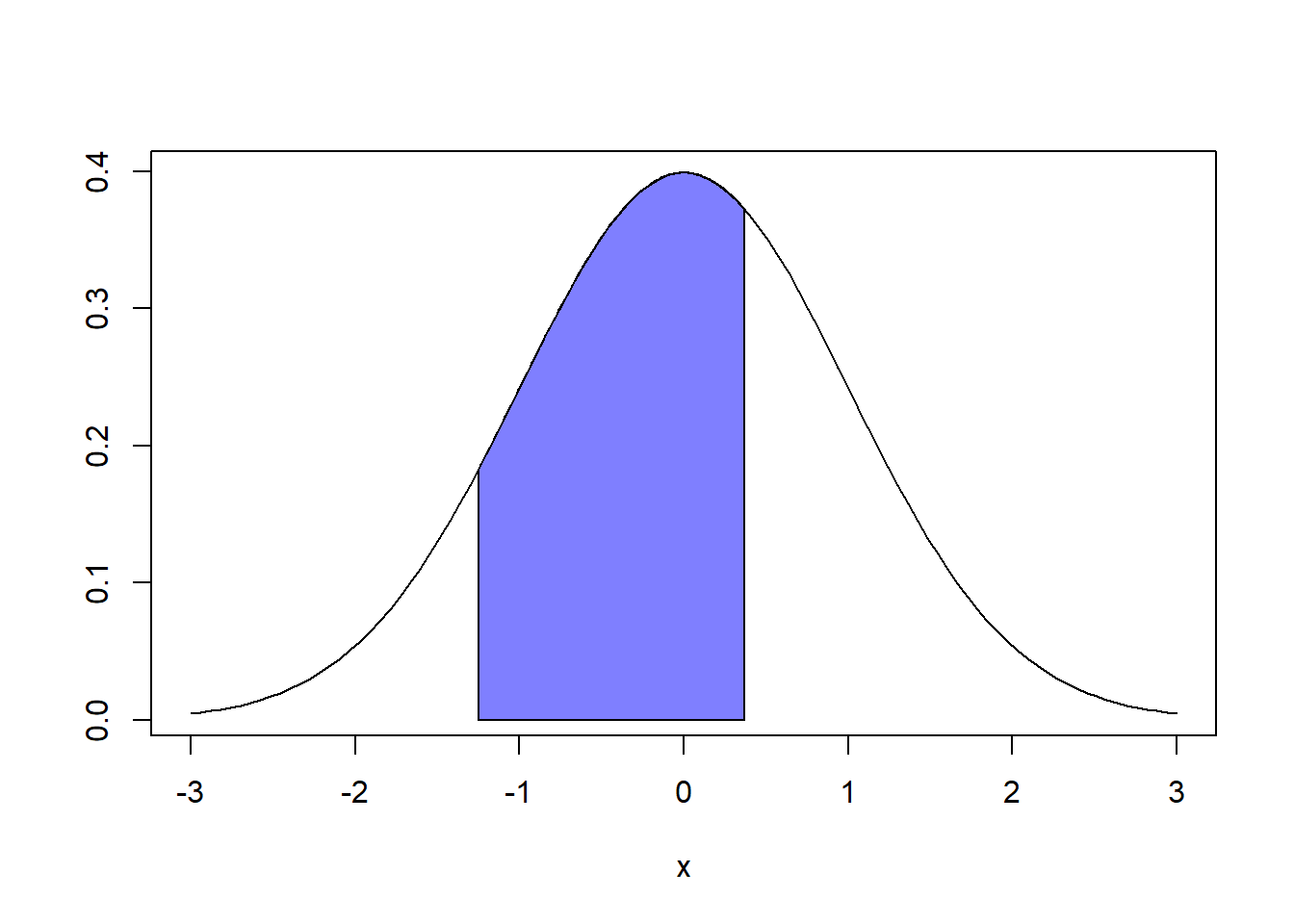 \[P(Z\leq 0.37)-P(Z\leq
-1.25)=0.6443-0.1056=0.5387\]
\[P(Z\leq 0.37)-P(Z\leq
-1.25)=0.6443-0.1056=0.5387\]
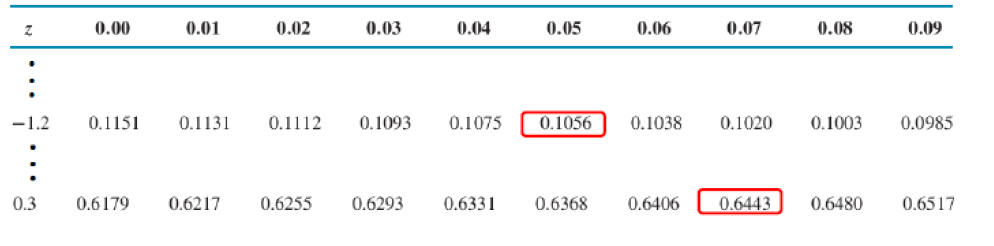
Ejemplo 5
\[P(Z>1.55)=1-P(z\leq 1.55)=1-0.9334=0.0666\]
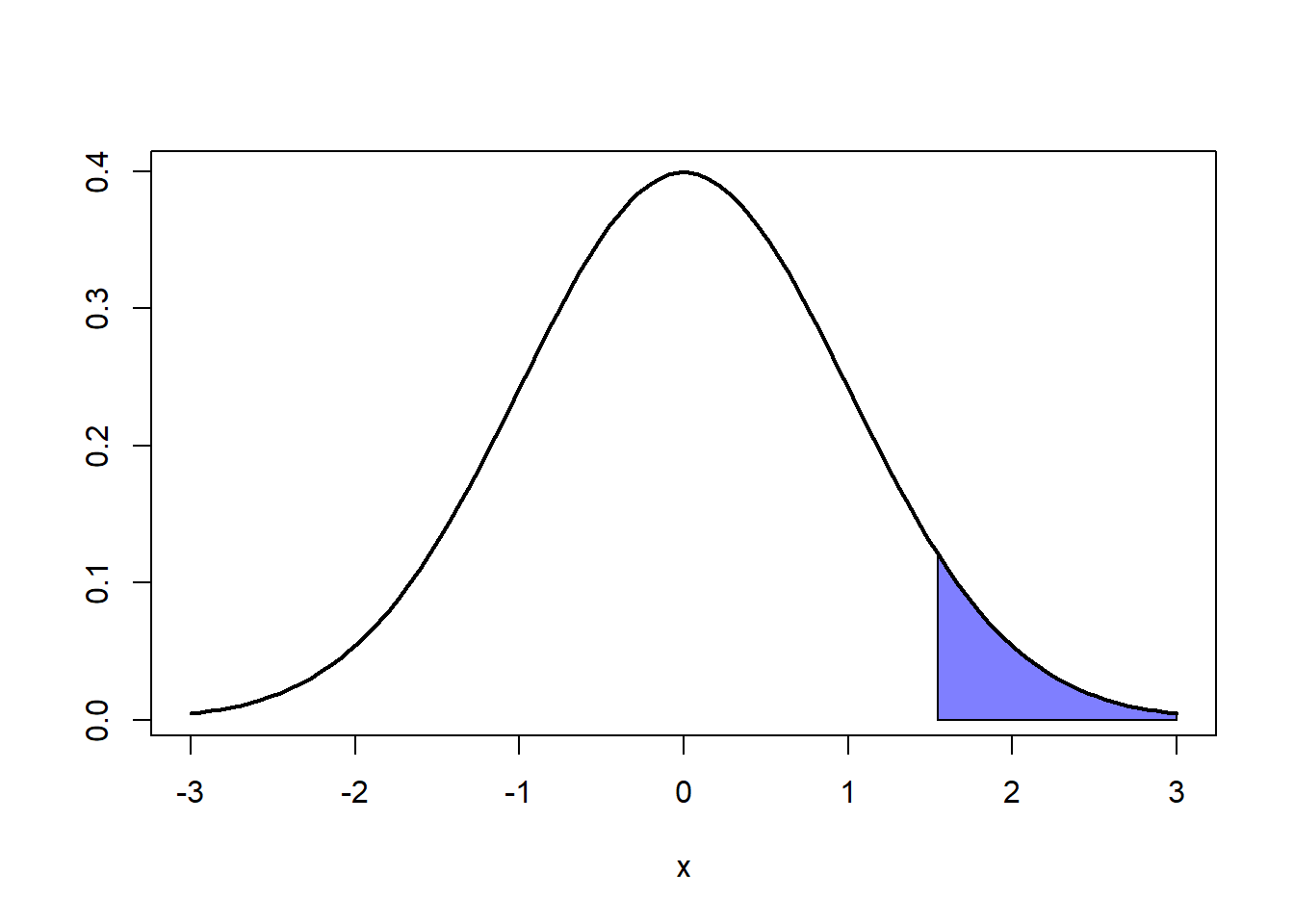

Ejemplo 6
\[P(-1.88<Z<0.46)=P(z\leq 0.46)-P(z \leq -1.88)=0.6772-0.0301\]
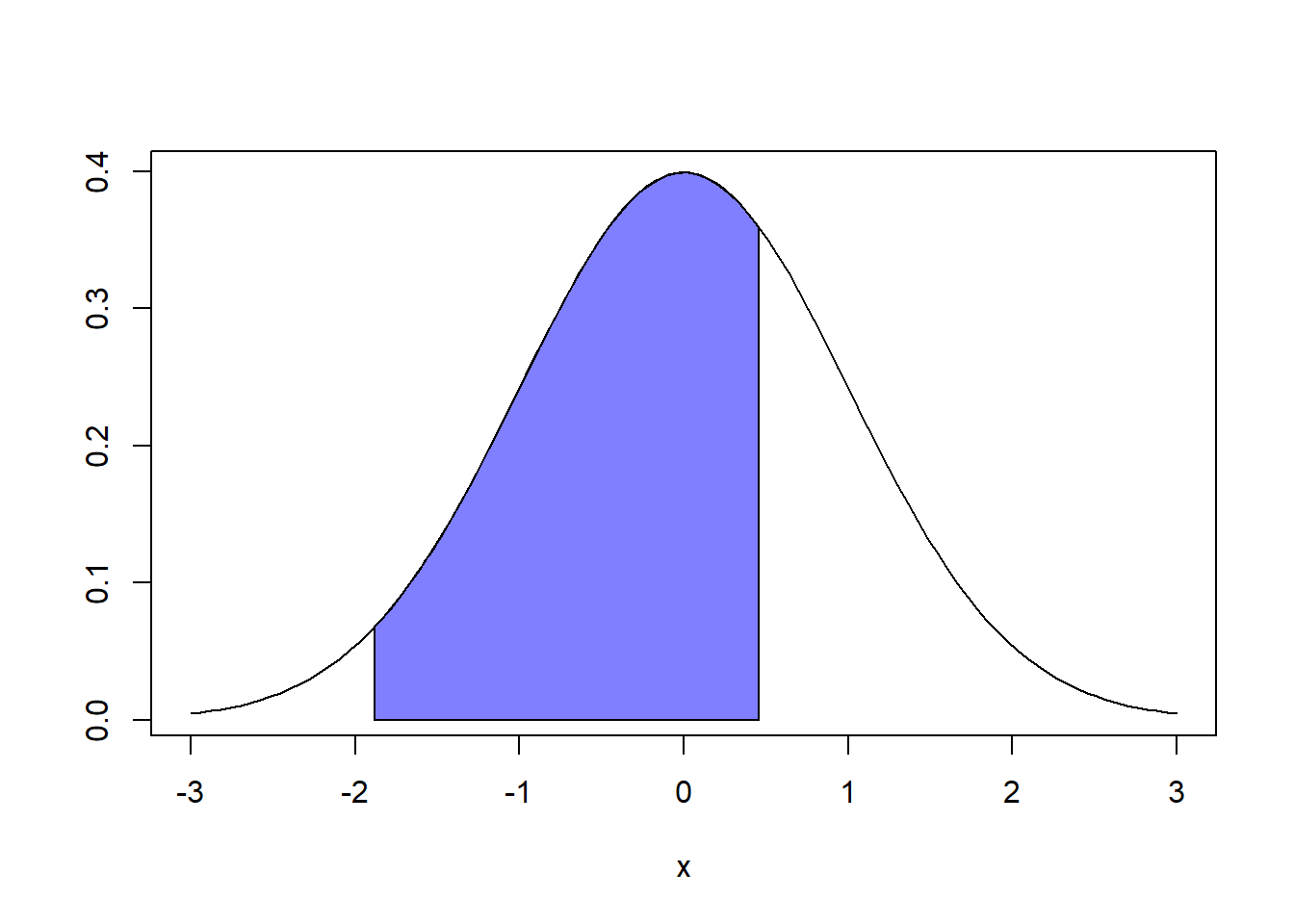
Ejemplo 7 La cantidad de café que vierte una máquina en jarras de 4 onzas varía de una jarra a otra, se puede fijar como una variable aleatoria que tiene una distribución normal con σ = 0,2 onzas.
¿Cuál es la probabilidad de que el contenido de una de las jarras este entre 3.5 y 3.8 onzas? Rta/ 0.1525
Cuál es la cantidad que caracteriza el 3% de las jarras con mayor contenido.
Cuál es la cantidad que caracteriza el 5% de las jarras con menor contenido.
Ejercicios \[\phi(c)=0.9838\] \[p(0\leq z \leq c)=0.291\] \[p(-c \leq z \leq c)=0.668\]
Ejemplo 8
Suponga que la fuerza que actúa en una columna que ayuda a soportar un edificio está normalmente distribuida con media de 15 kips y desviación estándar de 1,25 kips ¿ Cuál es la probabilidad de que la fuerza
Sea de más de 18 kips
Este entre 10 y 12 kips
Este entre 1.5 desviaciones estándar de la media
Difiera de 15.0 kips en cuando mucho 1.5 desviaciones estándar
Teorema del límite central
Si se toman muestras cada vez más grandes de cualquier población, entonces la media de la distribución muestral\(\bar x\), tiende a acercarse cada vez más a la verdadera media de la población \(\mu\). En la practica cuando n>30 se consideran medidas poblacionales.
Aplicativo de distribuciones de probabilidad discretas
casos en los que la distribución binomial se asemeja a una distribución normal
En la medida en que los tamaños muestrales aumentan, con \(p\neq 0.5\),
Cuando p=0.5 y los tamaños de muestra son grandes.
casos en los que la distribución poisson se asemeja a una distribución normal
- La distribución poisson se asemeja a una distribución normal en la medida en que la tasa de ocurrencia aumenta.
Aproximaciones
Cuando la distribución subyacente es discreta, la curva normal es una buena aproximación. Además, aun cuando las variables individuales no estén normalmente distribuidas, las sumas y promedios de las variables en condiciones adecuadas tendrán de manera aproximada una distribución normal, para lo cual se usa el factor de corrección por continuidad con valor \[\Large 0.5\] ## Casos de corrección por continuidad - \[P(x<k)=P(x\leq k-0.5)\]
\[P(x>k)=p(x>k+0.5)\]
\[P(x=k)=(p(k-0.5<k<k+0.5)\]
\[P(x\leq k)=P(x \leq k+0.5)\]
\[P(x\geq k)=1-p(\leq k-0.5\]
Aproximación normal a la binomial
La distribución binomial se asemeja a una distribución normal
En la medida en que los tamaños muestrales aumentan, con \(p\neq 0.5\),
Cuando p=0.5 y los tamaños de muestra son grandes.
recuerda que p+q=1
La normal es una buena aplicación si \(n>10\), \(np>5\), \(nq>5\), así los parámetros son:
\[\Large \mu=np\] \[\Large \sigma=\sqrt {npq}\] La variable aleatoria se denota de la forma
\[X_i\sim N(np, npq)\] Ejemplos Un hotel tiene 100 habitaciones, la probabilidad de que una habitación este ocupada una noche es de 0.6.
¿ cual es la probabilidad de que 75 habitaciones o mas estén ocupadas una noche?
Se tiene: n=100
p=0.6
np=60
nq=40
\(\mu=60\)
\(\Large \sigma=\sqrt {100*0.6*0.4}=4.89\)
Por la distribución binomial
\[\Large P(\geq 75)= \sum_{i=75}^{100}{100 \choose i }*0.6^i*0.4^{100-i}\] Por aproximación normal
\[\Large P(x\geq 75)=1-P(x<75)\] Aplicando factor de corrección
\[\Large =1-P(x<75-0.5)\] Estandarizar….
Aproximación normal a la distribución poisson
La distribución poisson se asemeja a una distribución normal en la medida en que la tasa de ocurrencia aumenta.
Si en una distribución poisson \(\lambda >25\), se puede usar la distribución normal con
\[\mu=\lambda \] \[\sigma =\sqrt \lambda \] La variable aleatoria se denota como \[X_i \sim N(\lambda, \lambda)\]
videos
Distribución normal
Taller
Distribución normal
- Hallar el área bajo la curva normal tipificada:
- Entre Z = 0 y Z = 1,2 Sol: 0,3849
- Entre Z = 0,81 y Z = 1,94 Sol: 0,1828
- A la derecha de Z = -1,28 Sol: 0,8997
- Si “área” se refiere al área bajo la curva normal tipificada, hallar el valor o los valores de Z tales que:
- El área entre 0 y Z sea 0,3770 Sol: Z = ±1,16
- El área a la izquierda de Z sea 0,8621 Sol: Z = 1,09
- El área entre -1,5 y Z sea 0,0217 Sol: Z = -1,69 y Z = -1,35
- El peso medio de 500 estudiantes varones de una universidad es de 68,5 Kg. y la desviación típica es de 10 Kg. Suponiendo que los pesos están distribuidos normalmente, hallar el número de estudiantes que pesan:
- Entre 48 y 71 kg. Sol: entre 289 y 290 estudiantes.
- Más de 91 kg. Sol: entre 6 y 7 estudiantes.
La media del diámetro interior del conjunto de lavadoras producidas por una máquina es 1,275 cm. y la desviación típica de 0,0125 cm. El propósito para el cual se han diseñado las lavadoras permite una tolerancia máxima en el diámetro de 1,26cm. a 1,29 cm., de otra forma las lavadoras se consideran defectuosas. Determinar el porcentaje de lavadoras defectuosas producidas por la máquina, suponiendo que los diámetros están distribuidos normalmente. Sol: 23,02%
Si X está distribuida normalmente con media 5 y desviación típica 2, hallar P (X > 8). Sol: 0,0668
Se tiene un programador de entrenamiento diseñado para mejorar la calidad de las habilidades de los supervisores de la línea de producción. Debido a que el programa es auto administrativo, los supervisores requieren un número diferente de horas para terminarlo. Un estudio de los participantes anteriores indica que el tiempo medio que se lleva completar el programa es de 500 h. y que esta variable aleatoria normalmente distribuida tiene una desviación estándar de 100 h.
¿Cuál es la probabilidad de que un participante elegido al azar requiera más de 500 h. para completar el programa?. Sol: 0,5
¿Cuál es la probabilidad de que un candidato elegido al azar se tome entre 500 h. y 650 h. para completar el programa de entrenamiento?. Sol: 0,4332
¿Cuál es la probabilidad de que un candidato elegido al azar se tome más de 700 h. en completar el programa?. Sol: 0,0228
Suponga que el director del programa de entrenamiento desea saber la probabilidad de que un participante escogido al azar requiera entre 550 y 650 h. para completar el trabajo requerido en el programa. ¿Cuánto ha de ser ese valor? Sol: 0,2417
¿Cuál es la probabilidad de que un candidato elegido al azar se tomará menos de 580 h. para completar el programa? Sol; 0,7881
¿Cuál es la probabilidad de que un candidato escogido al azar se tome entre 420h.y 570 h. para completar el programa? Sol: 0,5461
- Dada una variable con distribución normal de media μ = 40 y desviación estándar σ = 6 encuentre el valor de x que tiene:
- El 34% del área a la izquierda. Sol: 37,54
- El 5% del área a la derecha. Sol: 49,87
Cierto tipo de pieza para automóvil tiene un promedio de duración de tres años, con una desviación estándar de 0,5 años. Suponga que las duraciones de las piezas están normalmente distribuidas y encuentre la probabilidad de que una pieza determinada tenga un tiempo de duración de más de 3,5 años. Sol: 0,1587
Una fábrica de alimentos empaca productos cuyos pesos están normalmente distribuidos con media de 450 gramos y desviación estándar de 20 gramos. Encuentre la probabilidad de que un paquete escogido al azar pese entre 425 y 486 gramos. Sol: 0,8585
En un proceso industrial el diámetro de una arandela es muy importante. El comprador establece en sus especificaciones que el diámetro debe ser de 3,0 ± 0,01 mm. La condición es que no acepta ninguna arandela que se salga de estas especificaciones. Se sabe que en el proceso el diámetro de las arandelas tienen distribución normal con media de 3,0 mm y una desviación estándar de 0,005 mm. ¿Qué porcentaje de arandelas será rechazado?. Sol: 4,56%
Determine el área situada debajo de la curva normal estándar que está:
- A la izquierda de z = 0,94 Sol: 0,8264
- A la derecha de z = - 0,65 Sol: 0,7422
- A la derecha de z = 1,76 Sol: 0,0392
- A la izquierda de z = - 0,85 Sol: 0,1977
- Entre z = - 0,87 y z = - 1,28 Sol: 0,0919
- Entre z = - 0,34 y z = 0,62 Sol: 0,3655
- Determine las probabilidades de que una variable aleatoria tome un valor entre 12 y 15 dado que tenga una distribución normal con:
- μ = 10 y σ = 5 Sol: 0,1859
- μ = 20 y σ = 10 Sol: 0,0966
- Obtenga Z si:
- El área de la curva normal entre 0 y Z es 0,2019 Sol: Z=±0,53
- El área de la curva normal a la derecha de Z es 0,8810 Sol: Z=-1,18
- El área de la curva normal a la derecha de Z es 0,0336 Sol: Z= 1,83
- El área de la curva normal entre -Z y Z es 0,2662 Sol: Z =±0,34
- Una empresa fabrica juntas teóricas para el trasbordador espacial de la NASA. Las cuales se han diseñado para sellar conexiones y piezas en el sistema de combustible a fin de impedir fugas. Un tipo de juntas ha de tener 5 centímetros de diámetro para que encaje como es debido; no puede variar arriba o abajo en más de 0,25 cm. sin provocar una fuga peligrosa. La empresa afirma que esta junta tiene 5 cm. de media con una desviación típica de 0,17 cm. Si estas cifras son correctas y se supone una distribución normal de los diámetros, los funcionarios de la NASA desean determinar:
- La proporción de juntas que se adaptarán correctamente. Sol: 0,8584
- La proporción de juntas que son defectuosas. Sol: 0,1416
- La probabilidad de que cualquier junta tenga un diámetro superior a 5,3 cm. Sol: 0,0392
- La probabilidad de que una junta tenga un diámetro comprendido entre 4,9 y 5,2 cm. Sol: 0,6034
- La probabilidad de que una junta elegida al azar tenga un diámetro entre 5,3 y 5,5 cm. Sol:0,0376
- Un estudio reciente reveló que el 64% de las mujeres mayores de 18 años, consideran a la nutrición la prioridad en su vida. Se seleccionó una muestra de 60 mujeres. Determinar la probabilidad de que:
- 32 o más consideren importante la dieta diaria. Sol: 0,9686
- 44 o más estimen que la alimentación es esencial. Sol: 0,0853
- Más de 32 pero menos de 43 consideren importante el aspecto dietético. Sol: 0,8084
- Exactamente 44 consideren fundamental la alimentación. Sol: 0,0348
- Supóngase que X tiene una distribución probabilística binomial, con n = 50 y p = 0,25. Calcule:
- La media y la desviación estándar de la variable aleatoria. Sol: 12,5 y 3,06
- La probabilidad de que X valga 15 o más. Sol: 0,2578
- La probabilidad de que X valga 10 o menos. Sol: 0,2578
Ejercicios de aproximaciones
- En 2004 el estado de Florida resultó afectado por cuatro huracanes de gran intensidad. En 2005 un estudio indicó que en 2004, 48% de las familias en Florida no tenían planes para escapar de un huracán que se aproximaba. Suponga que una muestra aleatoria reciente de 50 familias se seleccionó en Gainesville y que los miembros de 29 de las familias indicaron que tenían un plan de escape en caso de huracán.
a Si los porcentajes estatales de 2004 todavía fueran válidos para las familias recientes de Gainesville, use la aplicación Normal Approximation to Binomial Distribution para determinar los valores exacto y aproximado de la probabilidad que 29 o más de las familias muestreadas tengan un plan de escape para el huracán.
b Consulte el inciso a. ¿La aproximación normal es cercana a la probabilidad binomial exacta? Explique por qué.
- Con base en su respuesta al Ejercicio anterior (a), ¿piensa usted que los porcentajes de 2004 de Florida todavía se aplican a las nuevas familias de Gainesville?
Una máquina se apaga para repararla si una muestra aleatoria de 100 piezas seleccionadas de la producción diaria de la máquina contiene al menos 15% de piezas defectuosas. (Suponga que la producción diaria es un número grande de piezas.) Si en un día determinado la máquina está produciendo sólo 10% de piezas defectuosas, ¿cuál es la probabilidad de que sea apagada? [Sugerencia: use la corrección de continuidad .5.]
Una línea aérea encuentra que 5% de las personas que hacen reservaciones para cierto vuelo no se presentan para el mismo. Si la línea aérea vende 160 boletos para un vuelo con sólo 155 asientos, ¿cuál es la probabilidad de que se disponga de un asiento para cada persona que tiene una reservación y piense volar? rta/0.898
4 De acuerdo con una encuesta realizada por la American Bar Association, 1 de cada 410 estadounidenses es abogado, mientras que 1 de cada 64 residentes en Washington, D.C. es abogado.
a Si se seleccionan aleatoriamente 1500 estadounidenses, ¿cuál es la probabilidad aproximada de que la muestra contenga al menos un abogado?
b Si la muestra se selecciona entre los residentes de Washington, D.C., ¿cuál es la probabilidad aproximada de que la muestra contenga más de 30 abogados?
c Si nos encontramos en una esquina en las calles de Washington, D.C. y entrevistamos a las primeras 1000 personas que pasan y 30 dicen que son abogados, ¿esto sugiere que la densidad de abogados que pasan por la esquina es mayor que la densidad dentro de la ciudad? Explique.
Un entrevistador piensa que 20% de los votantes de cierta zona están a favor de la emisión de bonos. Si 64 votantes se muestrean aleatoriamente de entre el gran número de electores de esta zona, calcule la probabilidad de que la fracción muestreada de votantes que están a favor de la emisión de bonos no difiera en más de 0.06 de la fracción real. Rta/0.7692
El gerente de un supermercado desea obtener información acerca de la proporción de clientes a quienes les disgusta la nueva política de hacer efectivos los cheques. ¿Cuántos clientes debe seleccionar si desea que la fracción muestral se encuentre a no más de .15 de la fracción real, con probabilidad de 0.98? Rta/ 61 clientes