Probabilidad
Conceptos
Experimento: Proceso al azar que produce un resultado sujeto a incertidumbre.
Espacio muestral (S):Conjunto de todos los posibles resultados de un experimento.
Evento:Subconjunto del espacio muestral, puede ser simple (un solo resultado), compuesto (mas de un resultado).
Definición
La probabilidad es una medida de la posible ocurrencia de un evento A.
\[P(A)=\frac{Numero\quad de\quad veces\quad del\quad evento A}{ Total\quad de \quad veces}\]
Propiedades
- Para cualquier evento \(0\leq P(A)\leq1\)
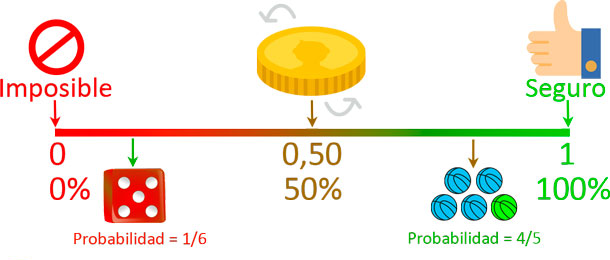
Probabilidad es un valor entre 0 y 1
\(P(S)=1\)
Si \(A_1, A_2, A_3 ...A_n\) es un conjunto de eventos mutuamente excluyentes entonces
\[P(A_1 U A_2 U A_3.. U A_n)=\sum_{i=1}^nP(A_i) \]
Teoría de conjuntos
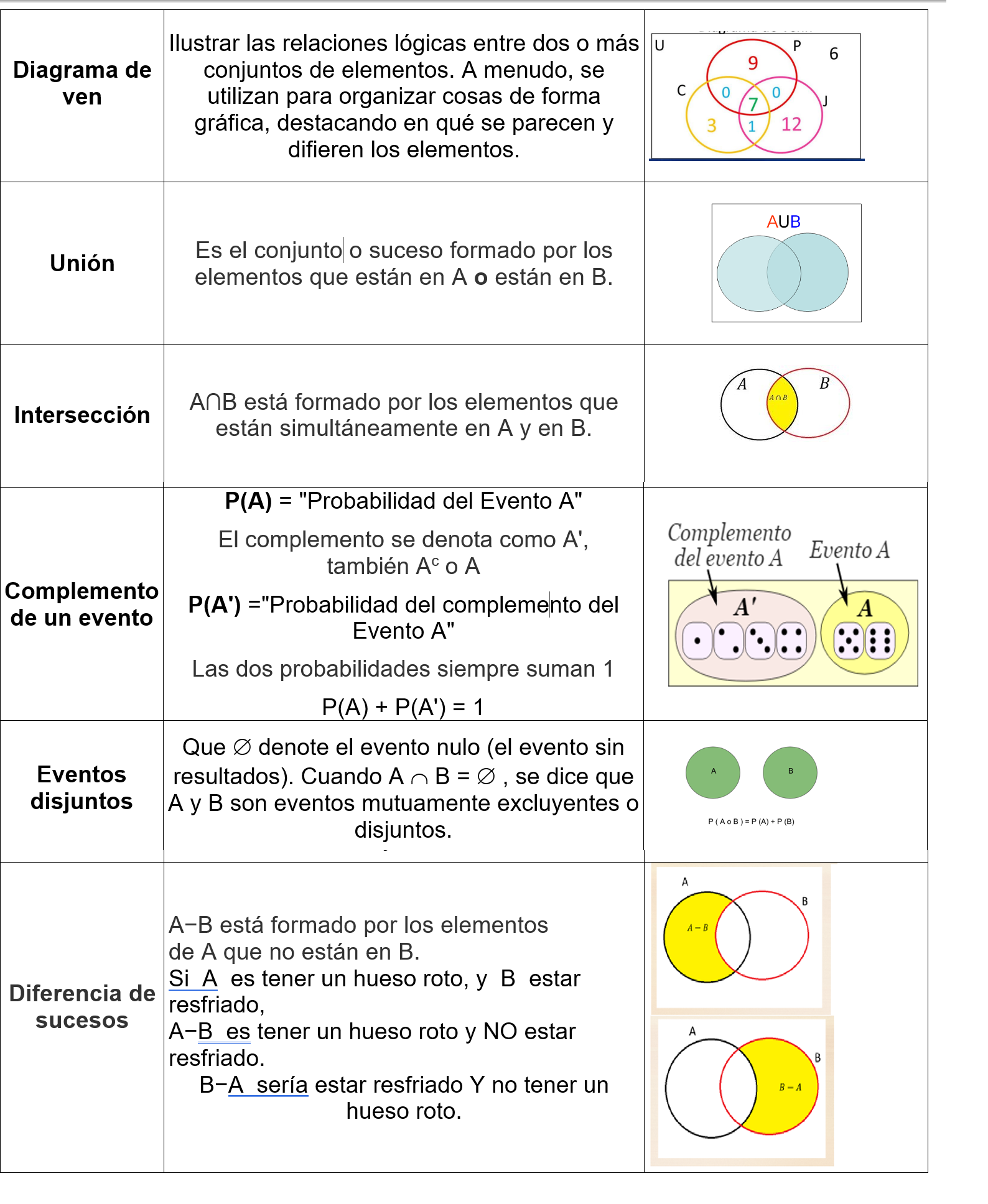
Teoría de conjuntos
Ejemplos clásicos de probabilidad
Ejemplo dos monedas
Se lanzan dos monedas y se observan los resultados posibles, obteniendo el siguiente espacio muestral.
\[S=\{(c,c),(c,s)(s,c)(s,s)\}\]
sea A el evento de obtener al menos una cara
\[A=\{(c,c),(c,s)(s,c)\}\]
sea B el evento de obtener al menos un sello
\[B=\{(s,s),(c,s)(s,c)\}\] Realice el diagrama de venn
Encuentre la probabilidad de los eventos
\[P(B)=P(A)=\frac{3}{4}\] ____________________________________________________________________________________________________
Ejemplo de 1 dado
Sea el espacio muestral comprendido por el resultado de la cara superior de un dado de 6 caras cuando se lanza
\[𝑺 = \{𝟏, 𝟐, 𝟑, 𝟒, 𝟓, 𝟔\}\]
Halle la probabilidad de que caiga una de las caras.
\[𝑃 (𝐴) =\frac{1}{6}\]
Sea B el evento de obtener un numero primo en la cara superior:
\[B= \{𝟐, 𝟑, 𝟓\}\]
Sea c el evento de obtener un numero par en la cara superior:
\[c= \{𝟐, 4,6\}\]
Sea d el evento de obtener un numero impar en la cara superior:
\[D= \{1,3,5\}\] Halle la probabilidad de cada uno de los eventos \[P(B)=P(C)=P(D)=\frac{3}{6}\]
Grafique el diagrama de ven
Encuentre el evento asi como su probabilidad \[B'\] \[CnB\] \[DnC\] \[BnCnD\]
\[BUCUD\]
Regla de la adición
\[P(AUB)=P(A)+P(B)-P(A\cap B)\]
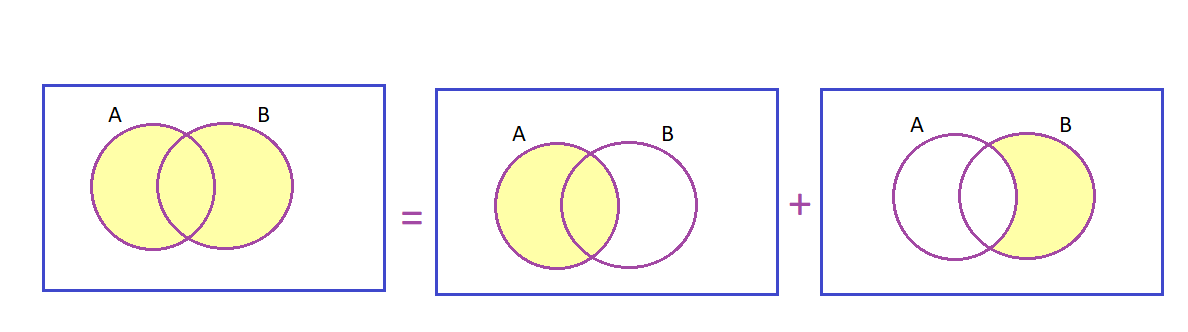
Teoría de conjuntos
Ejemplo 1
Se aplicó una encuesta a 50 personas sobre el consumo de gaseosas, obteniendo los siguientes resultados
20 prefieren coca cola
14 prefieren pepsi
5 no tienen preferencia por ninguno de ellos
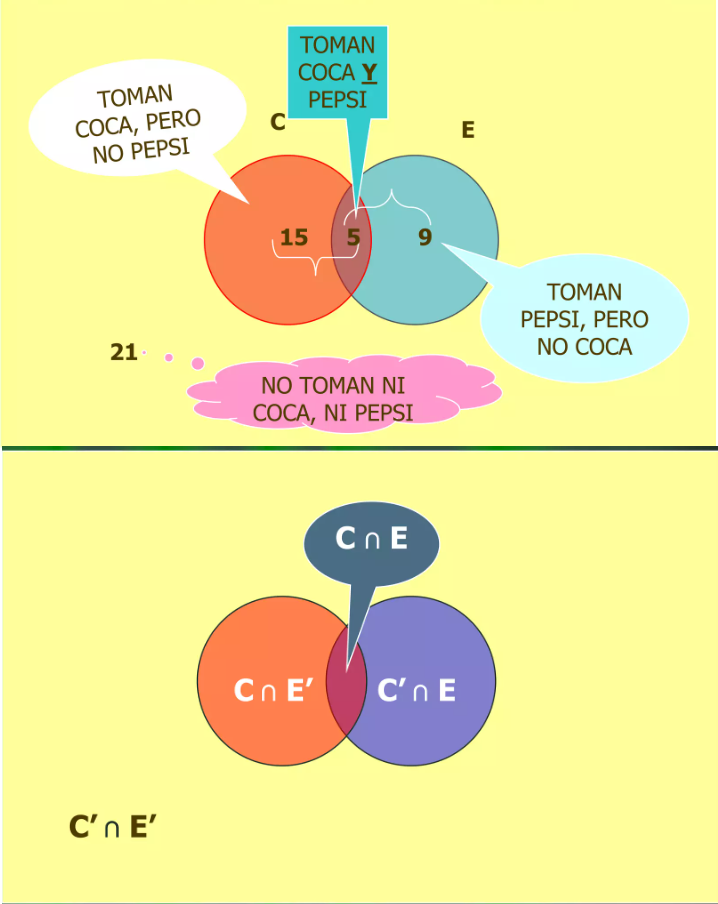
Teoría de conjuntos
Halle la probabilidad de:
cada uno de los eventos
Tome por lo menos un refresco
No tome ninguno de los refrescos
Cuál es la probabilidad de consumir solo una marca
\[P(C\cap E')+P(c'\cap E)\]
Ejemplo 2
Se hizo una encuesta en la ciudad sobre medio de transporte y se encontró que 70% usan servicios públicos de transporte, 40% usan transporte particular y 30% usan ambos tipos.
Realice el diagrama de venn
Calcular la probabilidad de
Usar solo un tipo de transporte
No usar ninguno de los medios de transporte
usar por lo menos un tipo de transporte
Video
Probabilidad condicional
\(P(A|B)\) Probabilidad de que suceda A, SI sucedió B
| Probabilidad de A dado B | Probabilidad de B dado A |
|---|---|
| \[P(A|B)=\frac{P(A\cap B)}{P(B)}\] | \[P(B|A)=\frac{P(A\cap B)}{P(A)}\] |
| este símbolo se lee como SI y dado que
P( Pregunta | condición)
\[P(A\cap B)=P(B\cap A)\] ______________________________________________________________________________________________________________________________________________
Ejemplo
Forma 1 Si salí en moto, ¿Cuál es la probabilidad de que llueva?
¿Cuál es la probabilidad de que llueva?, dado que salí en moto
\[P( llueva | moto)=\frac{P(llueva \cap moto)}{p(moto)}\] Forma 2 Si está lloviendo, ¿Cuál es la probabilidad de salir en moto?
¿Cuál es la probabilidad de salir en moto?, dado que está lloviendo
\[P( moto | llueva)=\frac{P(llueva \cap moto)}{p(llueva)}\]
Ejemplo
Se realizó una encuesta sobre hábitos de lectura que se resume por medio de la tabla.
| Género | Le gusta leer | No le gusta leer | total |
|---|---|---|---|
| Hombre | 40 | 20 | 60 |
| Mujer | 50 | 10 | 60 |
| Total | 90 | 30 | 120 |
Halle la probabilidad de que sea mujer
\[P(M)=\frac{60}{120}=0.5\]
HALLE LA PROBABILIDAD DE QUE SEA MUJER Y QUE LE GUSTE LEER? \[𝑃(𝐿 ∩ 𝑀) =\frac{50}{120}=0.42\]
2 formas de preguntar lo mismo:
forma 1: Halle la probabilidad de que lea dado que es mujer
forma 2:Si es mujer halle la probabilidad de que lea \[𝑃(𝐿|𝑀)=\frac{𝑃(𝐿∩𝑀)}{𝑃(𝑀)}=\frac{0.42}{0.5}\]
Probabilidad condicional
Independencia de eventos
Dos eventos son independientes si el resultado del segundo evento no es afectado por el resultado del primer evento.
\[P(A \cap B)=P(A)*P(B)\] \[P(A|B)= \frac{P(A\cap B)}{P(B)}\]
\[P(A|B)=P(A)\]
Teoría de conjuntos
Independencia de eventos
Otros ejemplos
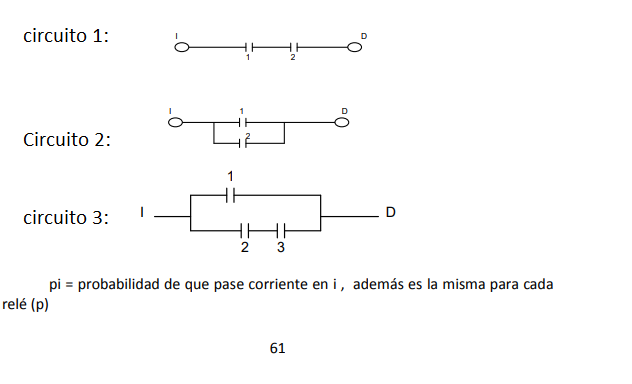
- Encuentre la probabilidad de que pase la corriente por cada uno de los circuitos mostrados en la figura, si la probabilidad de que cada relé este cerrado es p.
pi = probabilidad de que pase corriente en i , además es la misma para cada relé (p)
Teoría de conjuntos
Circuito 1
\[P (1 \cap 2) = p * p = p^2\]
Circuito 2 \[P(AUB)=P(A)+P(B)-P(AUB)\] \[p+p-p^2\] \[P(1U2)=p+p-p^2\]
Circuito 3
\[P(1U(2\cap 3)=P(1)+P(2\cap 3)-P(1\cap 2 \cap 3) \] \[p+(p*p)-p*p*p=p+p^2-p^3\]
Regla de la multiplicación
Si A y B son dos eventos cualesquiera en un espacio muestral S y P(A)≠0, entonces
\[P(B|A)=\frac{P(A\cap B)}{P(A)}\]
\[𝑃(𝐴)* 𝑃(𝐵|𝐴)=𝑃(𝐴 ∩ 𝐵)\]
Ejemplo
La urna A contiene 4 pelotas rojas y 3 azules, mientras que la urna B contiene 8 bolas rojas y 2 azules. Se toma una pelota de la urna A sin ver su color y se deposita en la urna B. Luego se toma una pelota de la urna B.
Calcular la probabilidad de que ambas pelotas elegidas de las urnas sean rojas, P(1R∩2R).

Teoría de conjuntos
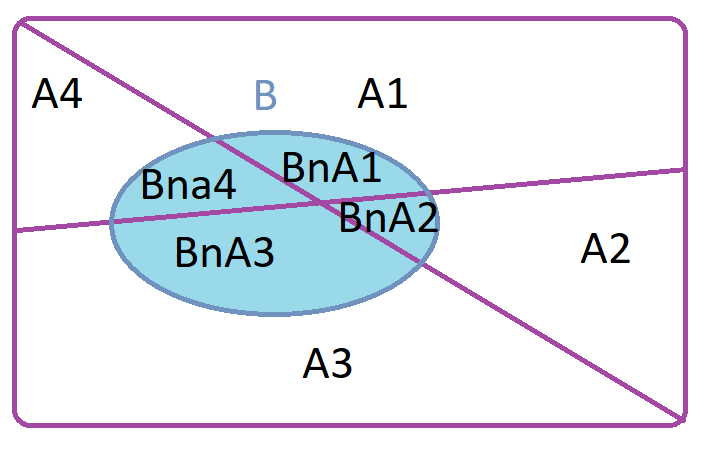
Regla de la probabilidad total
Sea \(A_1, A_2... A_k\) eventos mutuamente excluyentes de un espacio muestral S y para cualquier otro evento B, estaría definido como:
\[𝑃(B) = P(B∩A_1)+𝑃(B∩A_2)+ ⋯ + 𝑃(B∩A_k)\]
Teoría de conjuntos
\[𝑃(B)=𝑃(B|A_1)𝑃(A_1)+𝑃(B|A_2)𝑃(A_2)+⋯ + 𝑃(𝐵|A_𝐾)𝑃(A_𝐾)\]
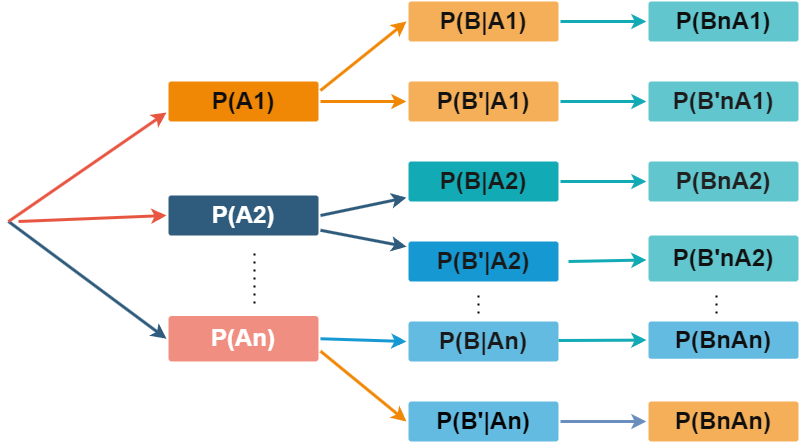
Teorema de bayes
Sea \(A_1, A_2... A_k\) eventos mutuamente excluyentes de un espacio muestral S con \(P(A_i)>0\) para \(i=1,2,3,...k\) y para cualquier otro evento B, en S Tal que \(P(B)>0\)
Teoría de conjuntos
\[P(A_1|B)=\frac{P(A_1\cap B)}{P(B)}\]
\[\frac{P(A_1)P(B|A_1)}{\sum_i^kP(A_i)P(B|A_i)}\]
Teorema de Bayes