Regresión lineal
Gráfico de dispersión
Diagrama matemático que utiliza las coordenadas cartesianas para mostrar los valores de dos variables cuantitativas, de la forma (x,y), aunque también se puede incluir una variable cualitativa. Sirve para la detección de puntos atípicos.
En el siguiente diagrama se ilustra la presión atmosférica en relación a la temperatura
plot(pressure)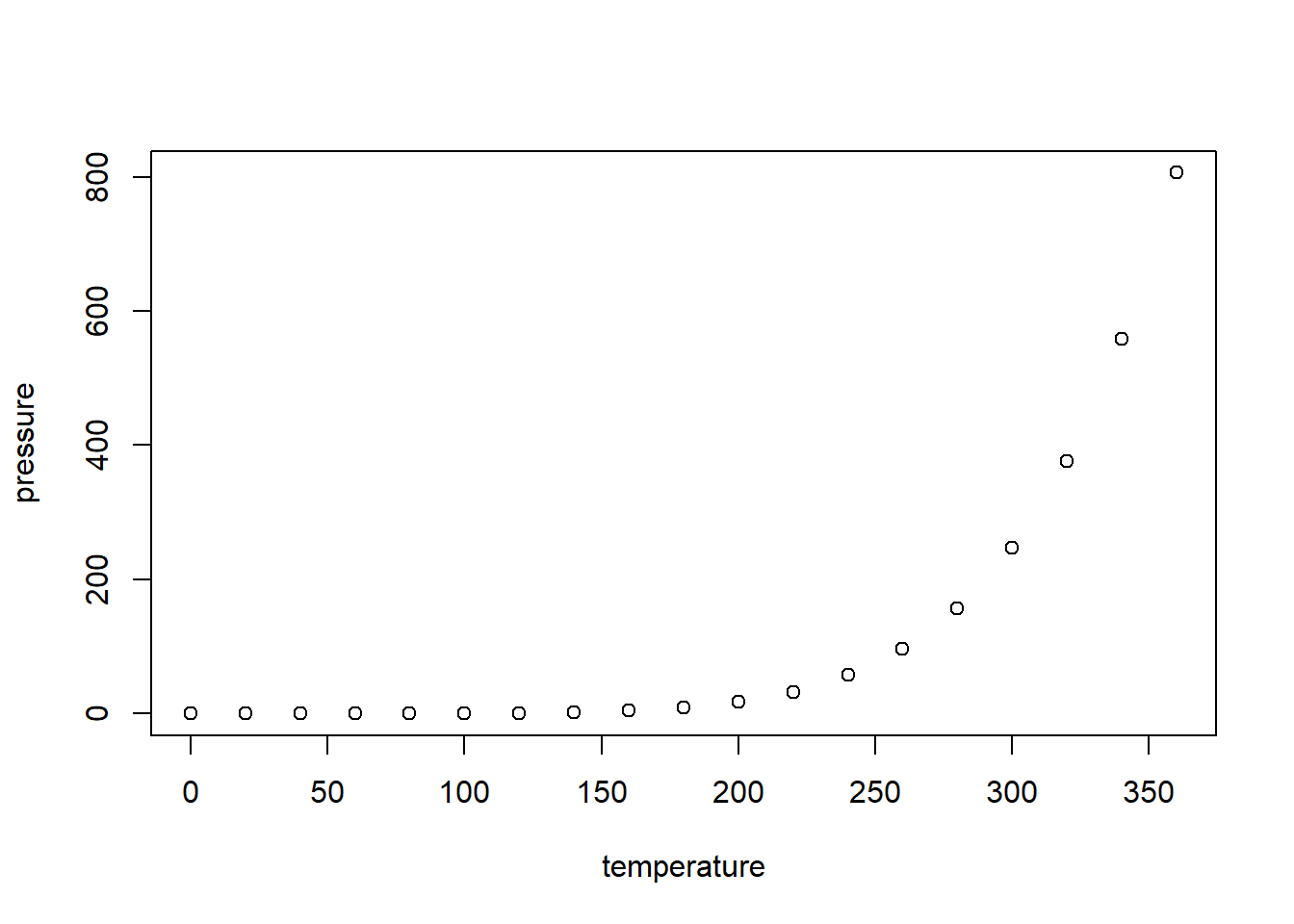
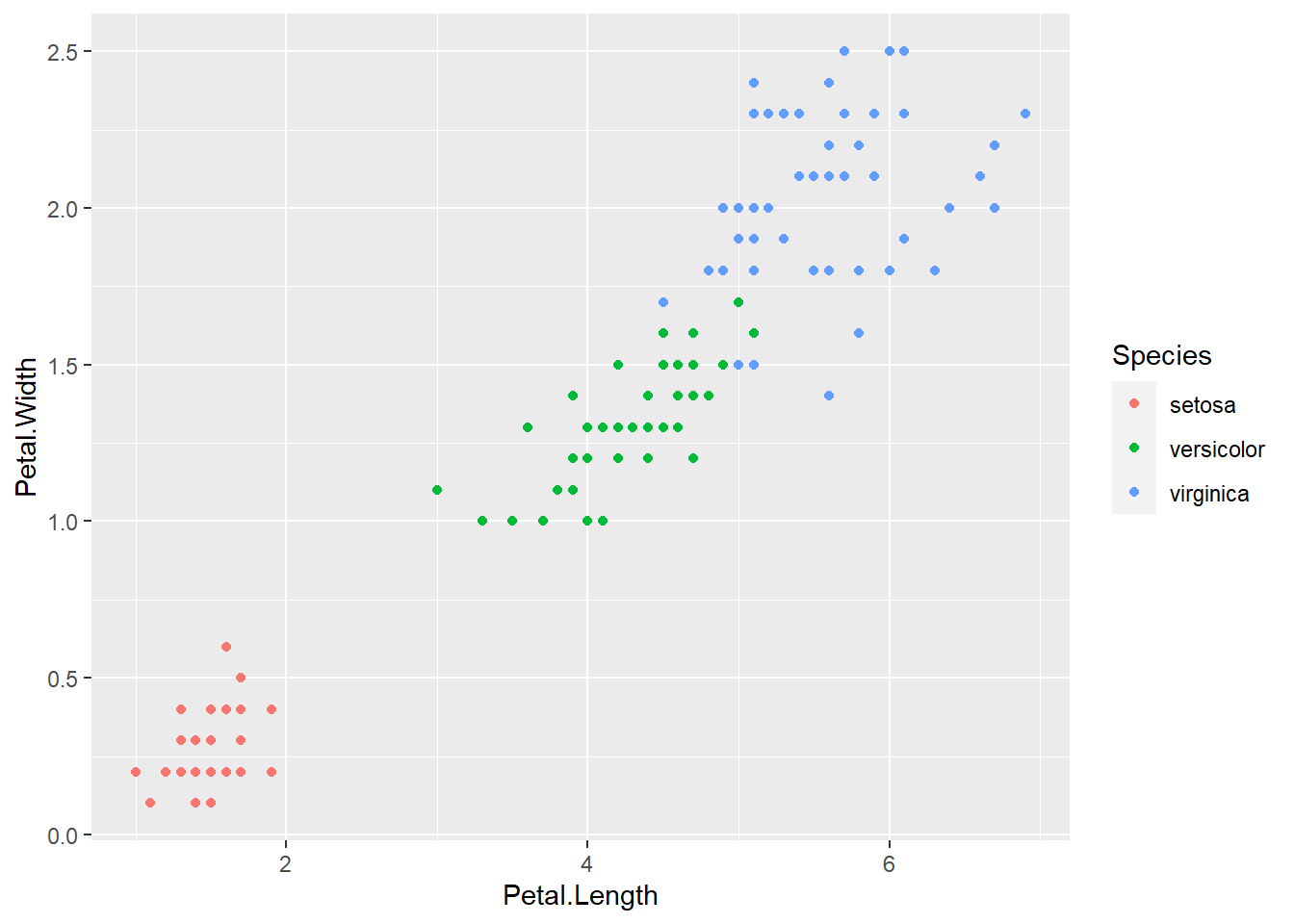
En el siguiente diagrama se ilustra el ancho y el largo de la hoja en relación al tipo de planta.
Actividad
Elabore en su cuaderno un gráfico de dispersión de los siguientes datos, identificando con colores diferentes el tipo de tapa.
| Hojas | Peso | Tipo de tapa |
|---|---|---|
| 885 | 800 | dura |
| 1016 | 950 | dura |
| 1125 | 1050 | dura |
| 239 | 350 | dura |
| 701 | 750 | dura |
| 641 | 600 | dura |
| 1228 | 1075 | dura |
| 412 | 250 | blanda |
| 953 | 700 | blanda |
| 929 | 650 | blanda |
| 1492 | 975 | blanda |
| 419 | 350 | blanda |
| 1010 | 950 | blanda |
| 595 | 425 | blanda |
| 1034 | 725 | blanda |
Regresión lineal
Permite establecer asociaciones entre variables de interés, entre las cuáles la relación usual no es necesariamente de causa efecto.
El objetivo es obtener estimaciones razonables de Y para distintos valores de X a partir de una muestra de n pares de valores (x1, y1), . . . ,(xn, yn).
Algunos ejemplos
Estudiar cómo influye la estatura del padre sobre la estatura del hijo.
Estimar el precio de una vivienda en función de su área.
Estudiar la relación entre el estrato de la vivienda y el pago del impuesto predial
Antes de hacer un modelo de regresión lineal
Se deben identificar observaciones extremas, alejadas hacia valores muy grandes o pequeños comparadas con el resto de valores, que puedan influenciar en la estimación de los parámetros del ajuste de regresión.
Modelo de regresión lineal básico
El modelo más simple de regresión corresponde a:
\[\Large y_i=\beta_0 +\beta_1 X_i+\varepsilon_i\] Donde:
\(\Large y_i\)Es la variable
respuesta o dependiente para la i-ésima observación
\(\Large \beta_0\) Intercepto
\(\Large\beta_1\) Pendiente
\(\Large X_i\) Variable predictora
independiente para la i-ésima observación
\(\Large \varepsilon_i\) Error
aleatorio para la i-ésima observación
\[\Large \varepsilon_i \sim N (0,\sigma^2)\]
Objetivos de la regresión lineal
Construir un modelo que describa el efecto o relación entre una variable X sobre otra variable Y.
Obtener estimaciones puntuales de los parámetros de dicho modelo.
Estimar el valor promedio de Y para un valor de X
Predecir futuros de la variable respuesta Y
Medidas de dependencia lineal
Covarianza
La covarianza indica el grado de variación conjunta de dos variables aleatorias respecto a sus medias
\[\Large cov(x,y)=\frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{(n-1)}\] - Si hay relación lineal positiva, la covarianza será positiva y grande.
Si hay relación lineal negativa, la covarianza será negativa y grande en valor absoluto.
Si no hay relación entre las variables la covarianza será próxima a cero.
La covarianza depende de las unidades de medida de las variables.
Coeficiente de correlación
Indica la fuerza y la dirección de una relación lineal y proporcionalidad entre dos variables cuantitativas estadísticas, la fórmula es:
\[\Large cor(x,y)=\frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})} {\sqrt{\sum_{i=1}^{n}(x_i-\bar{x})^2\sum_{i=1}^{n}(y_i-\bar{y})^2 }}\]
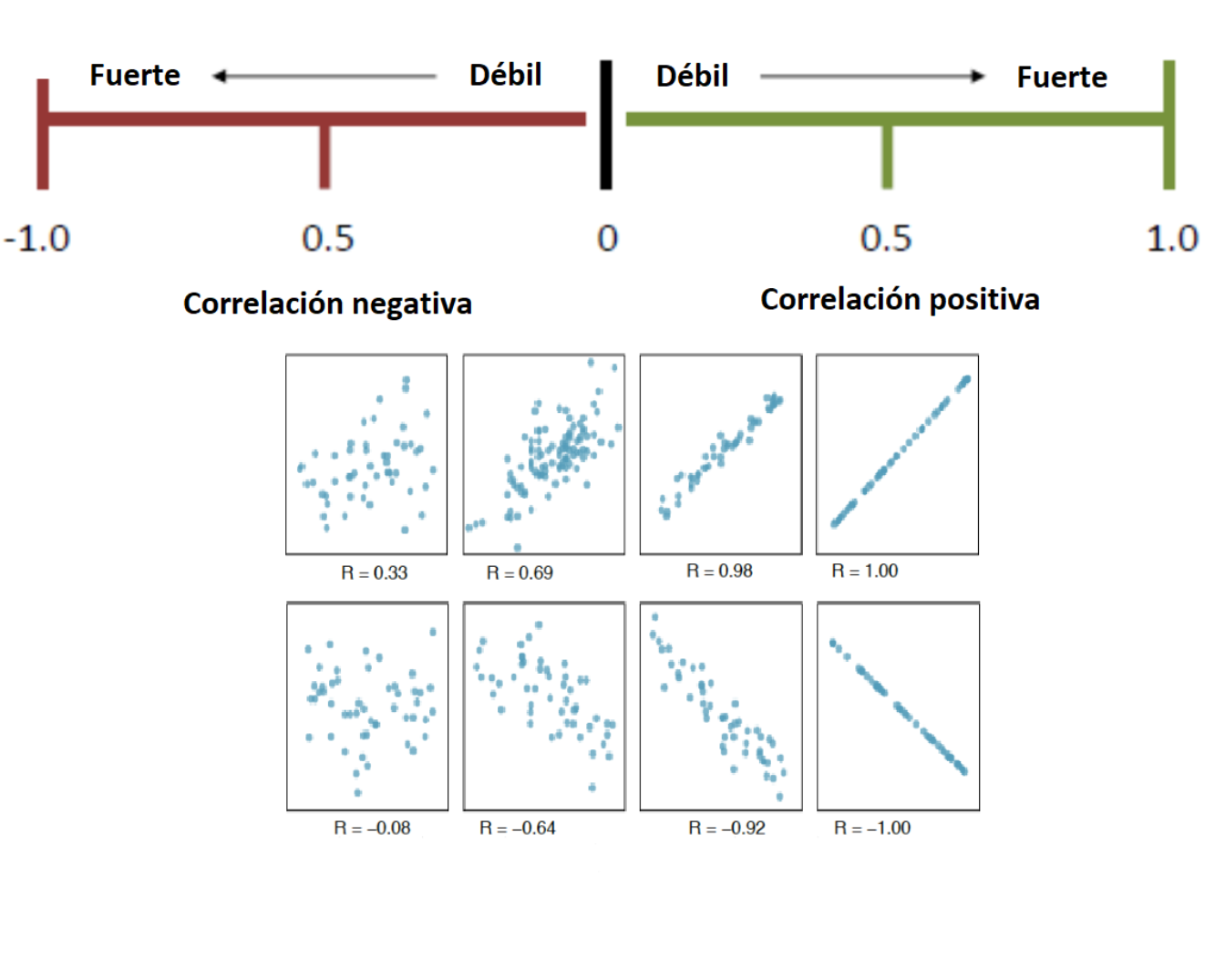
Características del coeficiente de correlación
Rango entre -1 y 1
Valores cercanos a -1 la relación es fuertemente negativa.
Valores cercanos a 1 la relación es fuertemente positiva.
Valores cercanos a 0 la relación es débil, es decir no hay una relación lineal
Medida de bondad de ajuste R^2
El coeficiente determina la calidad del modelo para replicar los resultados. Mide la proporción de la variabilidad total observada en la respuesta que es explicada por la asociación lineal. En regresión lineal el R cuadrado es simplemente el cuadrado del coeficiente de correlación de Pearson, Por ser una proporción, esta cantidad varía entre 0 y 1, mientras más cercano sea a uno mejor.
Estimador de mínimos cuadrados
Gauss propuso en 1809 el método de mínimos cuadrados para obtener los valores \(\hat{\beta_0}, \hat {\beta_1}\) que mejor se ajustan a los datos:
\[\Large y_i=\beta_0+\beta_1x_i+\varepsilon_i\]
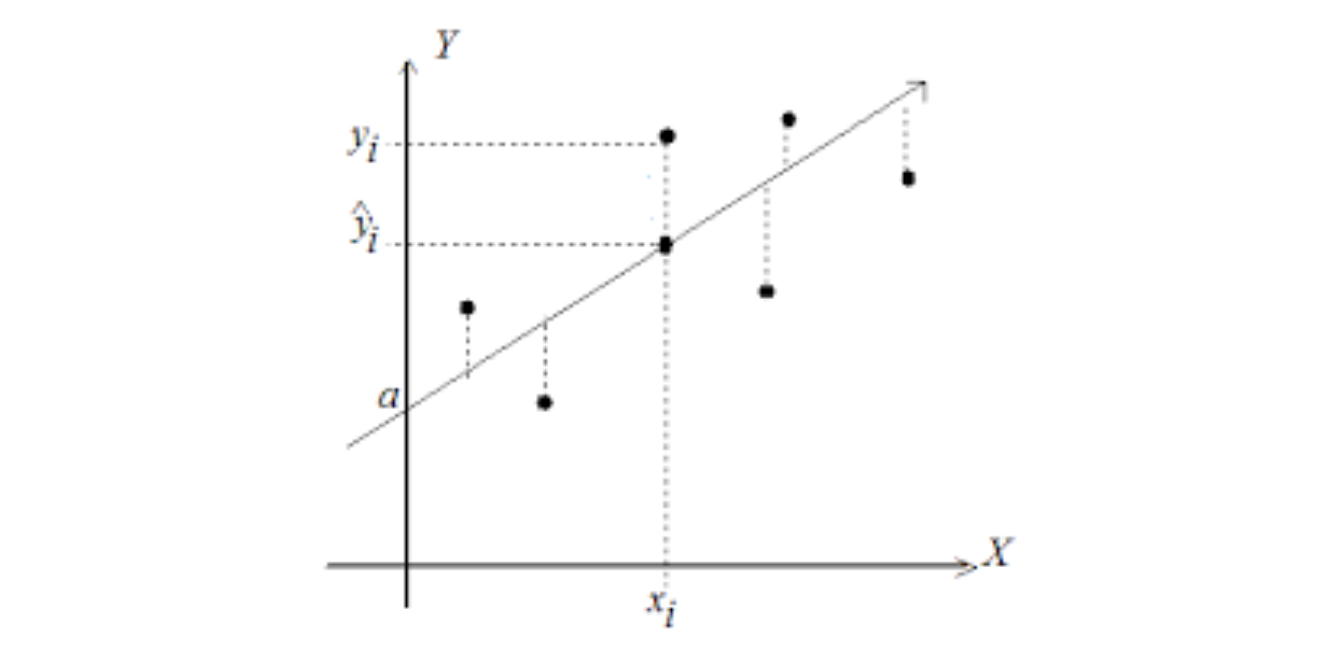
El método consiste en minimizar la suma de los cuadrados de las distancias verticales entre los datos y las estimaciones, es decir, minimizar la suma de los residuos al cuadrado:
\[\sum_{i=1}^n(y_i-\hat{y_i})^2= \sum_{i=1}^n (y_i-(\hat{\beta_0}+ \hat{\beta_1}x_i))^2\]
El resultado que se obtiene es:
\[\Large \hat{\beta_1}=\frac{S_{xy}}{S_{xx}}=\frac{cov(x,y)}{S_{xx}}=\frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^{n}(x_i-\bar{x})^2}\]
A las cantidades \(\Large S_{xx}\) y \(\Large S_{xy}\) se les conoce como suma corregida de cuadrados y suma corregida de productos cruzados de x y y, respectivamente
\[\Large \hat{\beta_0}=\bar{y}-\hat{\beta_1}\bar{x}\]
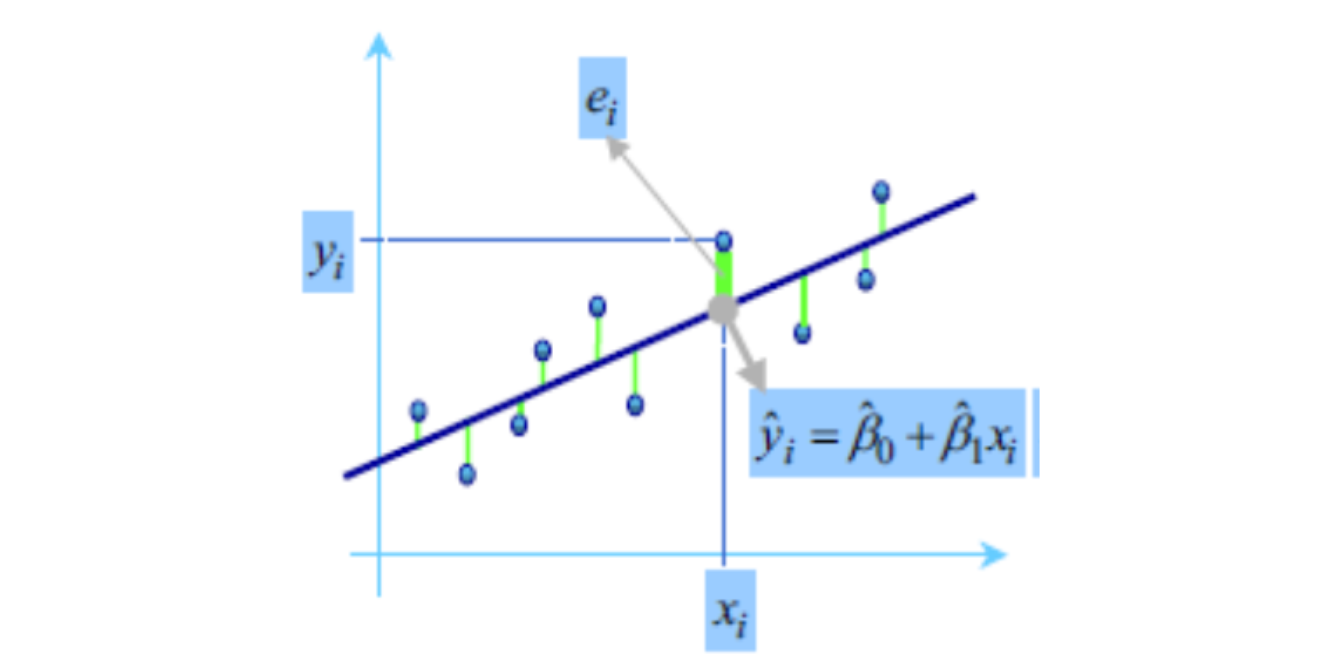
Residuales
La diferencia de cada valor \(y_i\) de la variable respuesta y su estimación \(\hat{y_i}\) se llama residuo. \[\Large \varepsilon_i= y_i- \hat{y_i}\]
Cómo obtener un modelo de regresión lineal simple
- Cómo estimar un modelo de regresión lineal en la calculadora
- Cómo estimar un modelo de regresión lineal en Excel
Regresión lineal múltiple
Considere el caso en el cual se desea modelar la variabilidad total de una variable respuesta de interés, en función de relaciones lineales con dos o más variables predictoras, cuantitativas o cualitativas, formuladas simultáneamente en un único modelo. Suponemos en principio que las variables predictoras guardan poca asociación lineal entre sí, es decir, cada variable predictora aporta información independiente de las demás predictoras presentes en el modelo (hasta cierto grado, la información aportada por cada una no es redundante). La ecuación del modelo de regresión en este caso es:
\[\Large y_i=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+...+\beta_kx_{ik}\varepsilon_i\]
Tipos de variables y de efectos en los modelos
Las variables predictoras pueden ser:
Cuantitativas, caso en el cual se supone se miden sin error (o el error es despreciable).
Cualitativas o categóricas, en este caso su manejo en el modelo se realiza a través de la definición de variables indicadoras, las cuales toman valores de 0 ó 1.
Por ejemplo, suponga que en un modelo de regresión para el gasto mensual por familia en actividades recreativas, se tiene entre las variables predictoras el estrato socioeconómico, definido en cinco niveles, luego, para cada nivel se define una variable indicadora de la siguiente forma:
Estrato 1: \[ \Large I_1 =\left\lbrace \begin{array}{rcl} {1\quad familia \quad estrato \quad 1} \\ {0 \quad En \quad otro \quad caso } \end{array} \right. \]
Estrato 2
\[ \Large I_2 =\left\lbrace \begin{array}{rcl} {1\quad familia \quad estrato \quad 2} \\ {0 \quad En \quad otro \quad caso } \end{array} \right. \] Estrato 3
\[ \Large I_3 =\left\lbrace \begin{array}{rcl} {1\quad familia \quad estrato \quad 3} \\ {0 \quad En \quad otro \quad caso } \end{array} \right. \]
Estrato 4 \[ \Large I_4 =\left\lbrace \begin{array}{rcl} {1\quad familia \quad estrato \quad 4} \\ {0 \quad En \quad otro \quad caso } \end{array} \right.\]
En general, una variable cualitativa con c clases se representa mediante c -1 variables indicadoras, puesto que cuando en una observación dada, todas las c-1 primeras indicadoras son iguales a cero, entonces la variable cualitativa se haya en su última clase. En el ejemplo anterior basta definir las primeras cuatro indicadoras.
Ejemplo:
La siguiente base de datos relaciona 7 medidas del crecimiento de 5 tipos de arboles en el tiempo en meses y el diámetro en mm.
library(ggplot2)
library(tidyverse)
library(viridis)
library(pacman)
p_load("datasets","DT", "fdth","prettydoc","xfun")
library(datasets)
bass=datasets::Orange
head(bass)## Grouped Data: circumference ~ age | Tree
## Tree age circumference
## 1 1 118 30
## 2 1 484 58
## 3 1 664 87
## 4 1 1004 115
## 5 1 1231 120
## 6 1 1372 142El diagrama de dispersión simple es:
plot(bass$age,bass$circumference,lwd=3)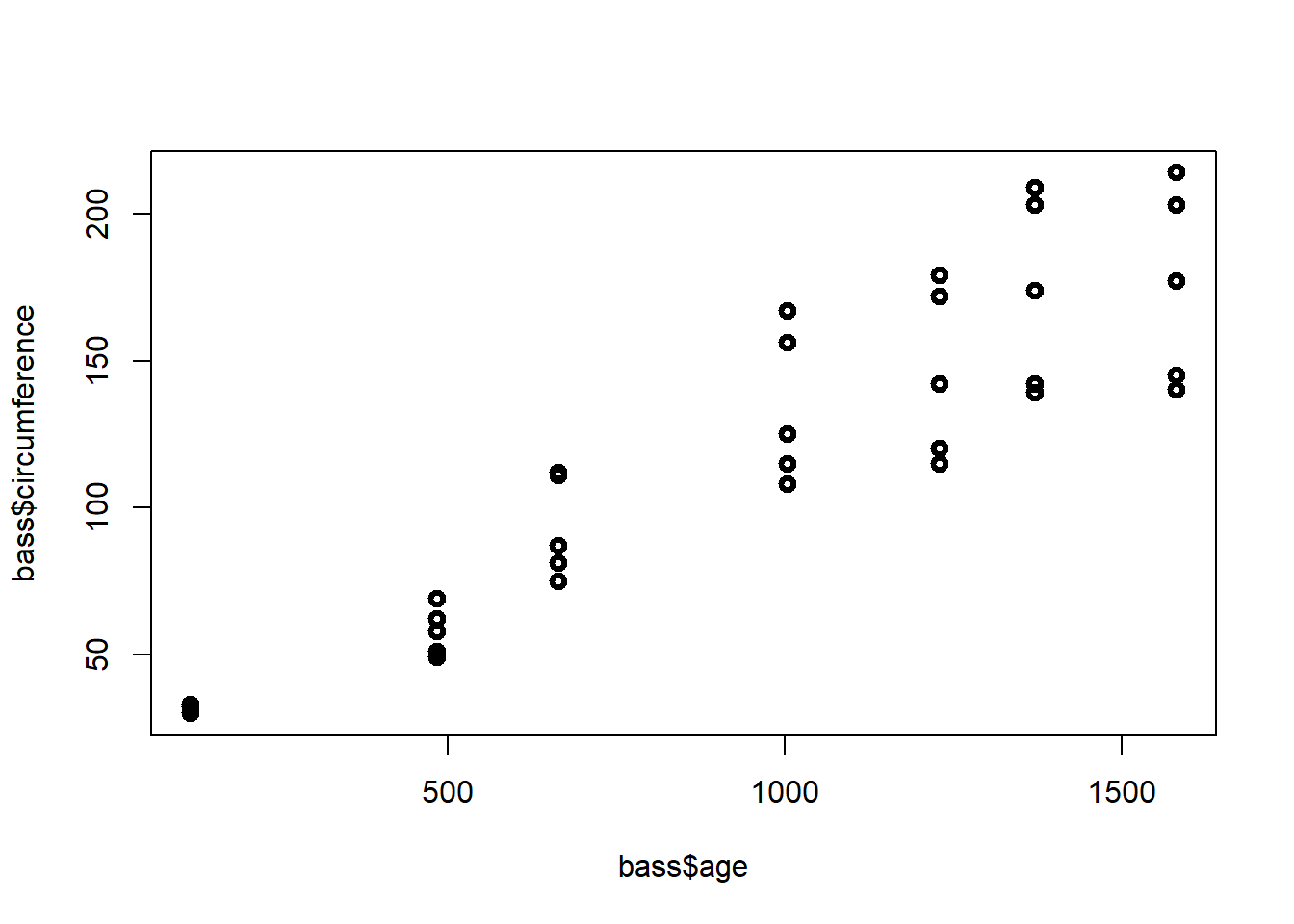
El modelo de regresión lineal simple corresponde a:
model=lm(bass$circumference~bass$age)
summary(model)##
## Call:
## lm(formula = bass$circumference ~ bass$age)
##
## Residuals:
## Min 1Q Median 3Q Max
## -46.310 -14.946 -0.076 19.697 45.111
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 17.399650 8.622660 2.018 0.0518 .
## bass$age 0.106770 0.008277 12.900 1.93e-14 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 23.74 on 33 degrees of freedom
## Multiple R-squared: 0.8345, Adjusted R-squared: 0.8295
## F-statistic: 166.4 on 1 and 33 DF, p-value: 1.931e-14La ecuación del modelo de regresión general es:
\[\Large \hat y_i=17.4+0.1x_{i}\] Donde \(y_i\) es la circunferenciua del
La linea de regresión ajustada corresponde a
model=lm(bass$circumference~bass$age)
plot(bass$age,bass$circumference,lwd=3)
yest=fitted(model)
lines(bass$age,yest,col=2)
abline(coef(model))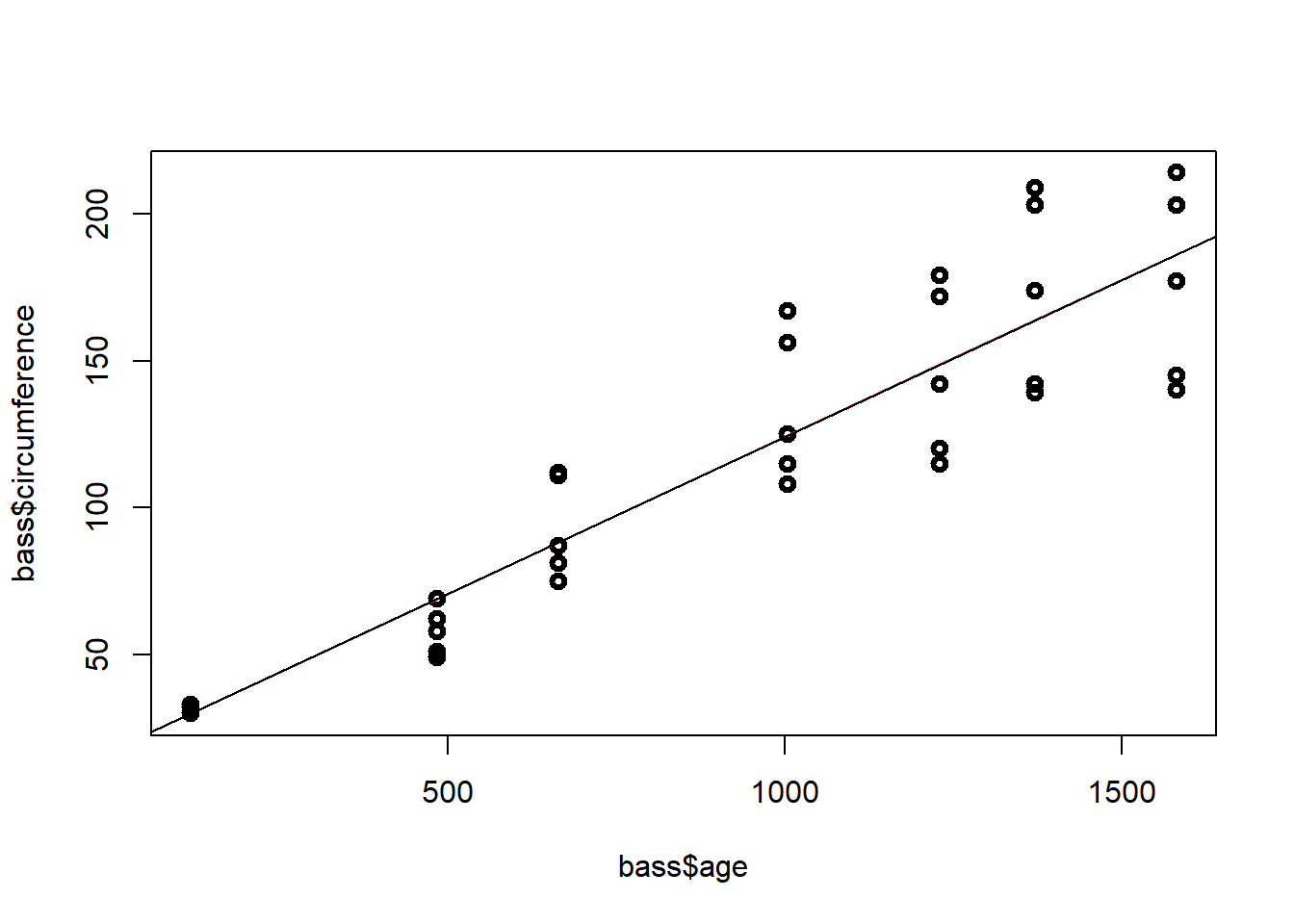
Significado de la pendiente y el intercepto
El intercepto es la respuesta media observada en el crecimiento de los arboles.
La péndiente indica que por cada mes que pasa la circunferencia del arbol aumenta 0.1 unidades
El diagrama de dispersión discriminando por los niveles de la variables factor es:
plot(bass$age,bass$circumference,col=bass$Tree,lwd=3)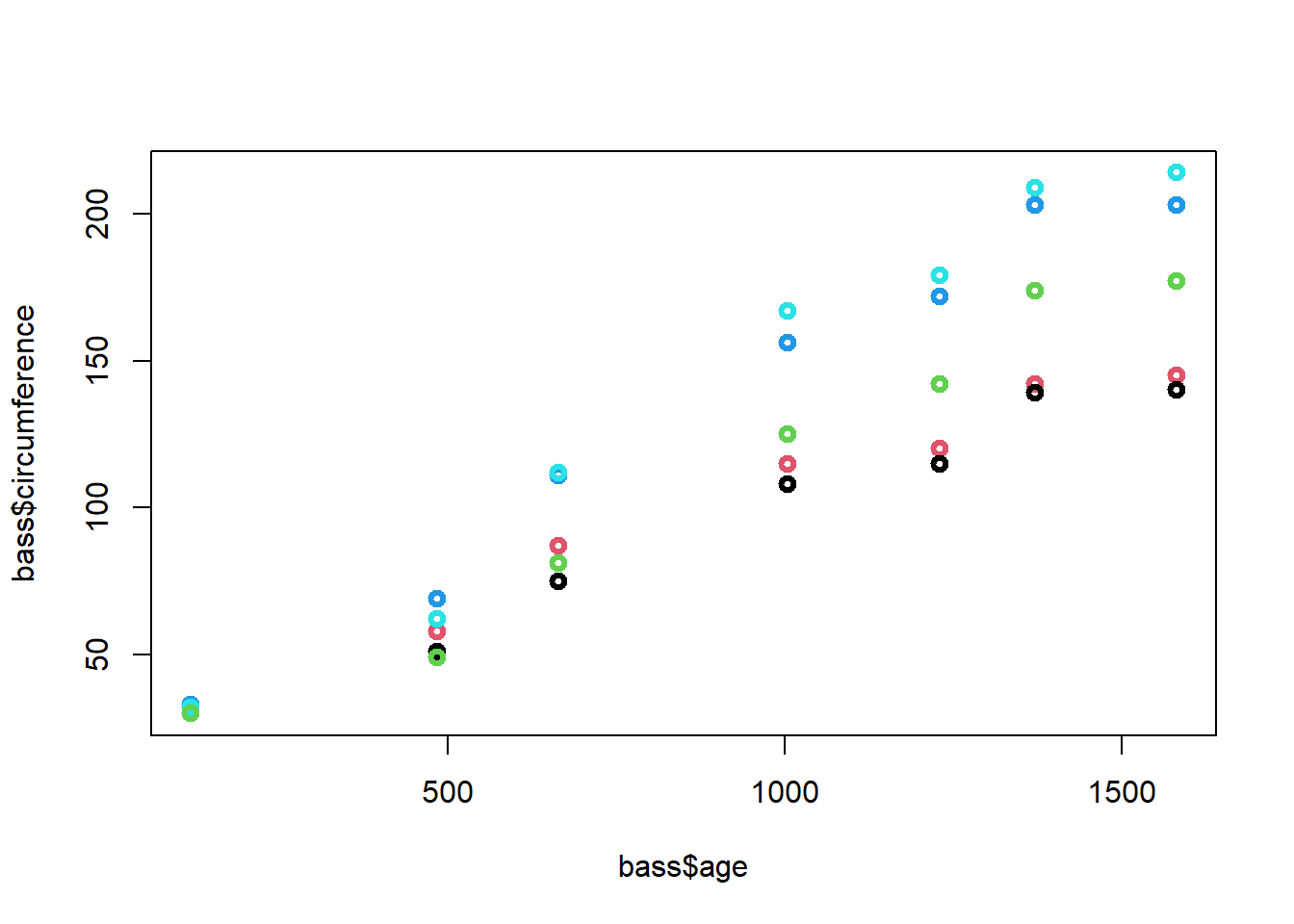
El modelo de regresión lineal con factores corresponde a
model=lm(bass$circumference~bass$age+as.factor(bass$Tree))
summary(model)##
## Call:
## lm(formula = bass$circumference ~ bass$age + as.factor(bass$Tree))
##
## Residuals:
## Min 1Q Median 3Q Max
## -30.505 -8.790 3.737 7.650 21.859
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 17.399650 5.543461 3.139 0.00388 **
## bass$age 0.106770 0.005321 20.066 < 2e-16 ***
## as.factor(bass$Tree).L 39.935049 5.768048 6.923 1.31e-07 ***
## as.factor(bass$Tree).Q 2.519892 5.768048 0.437 0.66544
## as.factor(bass$Tree).C -8.267097 5.768048 -1.433 0.16248
## as.factor(bass$Tree)^4 -4.695541 5.768048 -0.814 0.42224
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 15.26 on 29 degrees of freedom
## Multiple R-squared: 0.9399, Adjusted R-squared: 0.9295
## F-statistic: 90.7 on 5 and 29 DF, p-value: < 2.2e-16La recta general del modelo es:
\[\Large \hat y_i=17.4+0.1x_{i}+39.93arbol2_i+2.51arbol3_i-8.26arbol4_i-4.69arbol5_i\]
Las rectas ajustadas para cada arbol son:
Arbol 1:
\[\Large \hat y_i=17.4+0.1x_{i}\]
Arbol 2: \[\Large \hat y_i=57.33+0.1x_{i}\] Arbol 3: \[\Large \hat y_i=19.92+0.1x_{i}\]
Arbol 4: \[\Large \hat y_i=9.14+0.1x_{i}\] Arbol 5: \[\Large \hat y_i=12.71+0.1x_{i}\]