Distribuciones muestrales y el teorema de límite central
Distribuciones muestrales para una sola muestra
Un estadístico es una función de las variables aleatorias observables en una muestra, como la media muestral \(\bar Y\), la varianza muestral \(S^2\), Max, Min, la amplitud (Rango = max – min), la mediana muestral, etc.
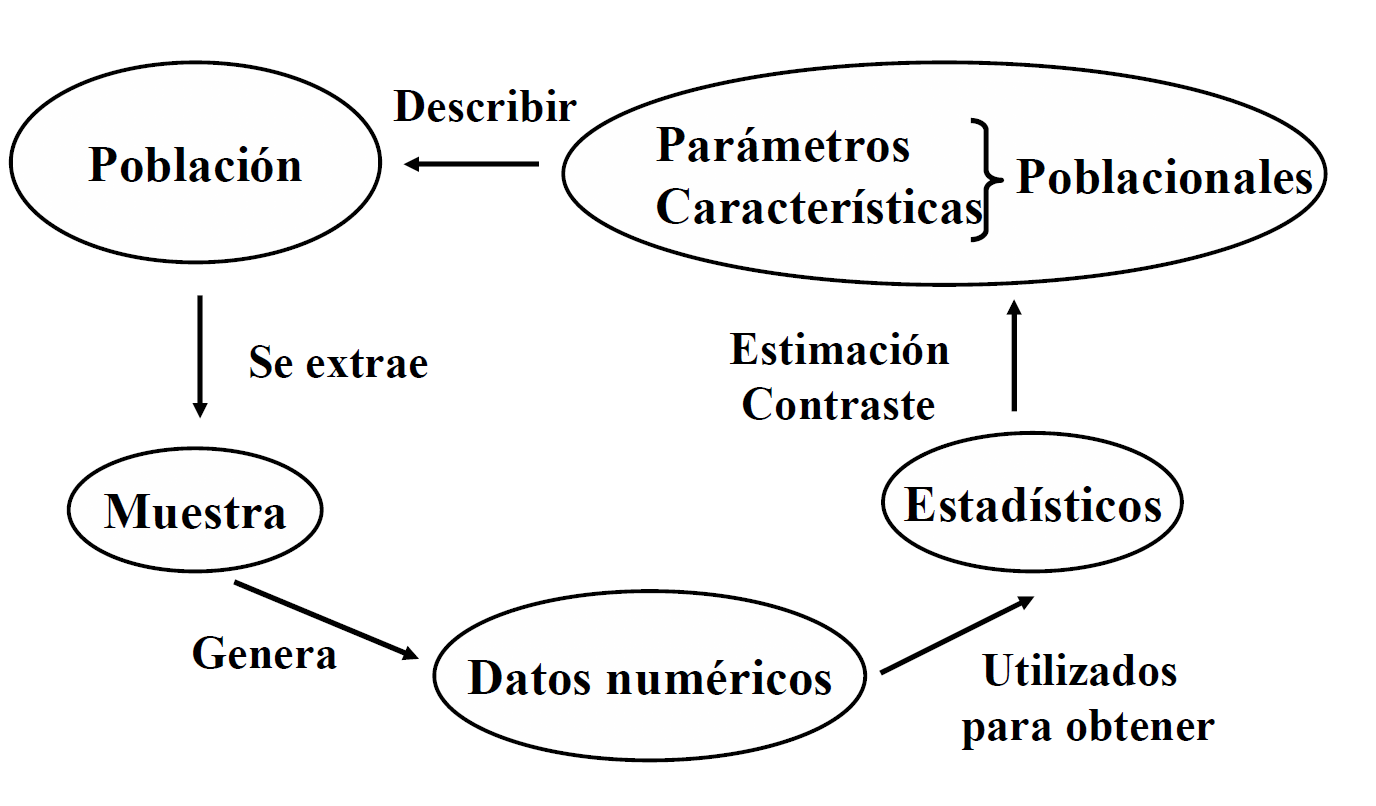
Se usan estadísticos para hacer inferencias o estimaciones, acerca de parámetros de población desconocidos. Todos los estadísticos son funciones de las variables aleatorias observadas en una muestra, por tanto también son variables aleatorias. En consecuencia, todos los estadísticos tienen distribuciones de probabilidad, que llamaremos distribuciones muestrales.
La distribución muestral de un estadístico proporciona un modelo teórico para el histograma de frecuencia relativa de los posibles valores del estadístico que observaríamos por medio de muestreo repetido.
Distribución muestral de medias
Si se seleccionan muestras aleatorias de tamaño 20 en una población grande. Se calcula la media muestral \(\bar X\) para cada muestra; la colección de todas estas medias muestrales recibe el nombre de distribución muestral de medias, así como tambien se puede obtener la distribución muestral de las desviaciones estándar lo que se puede ilustrar en la siguiente figura:
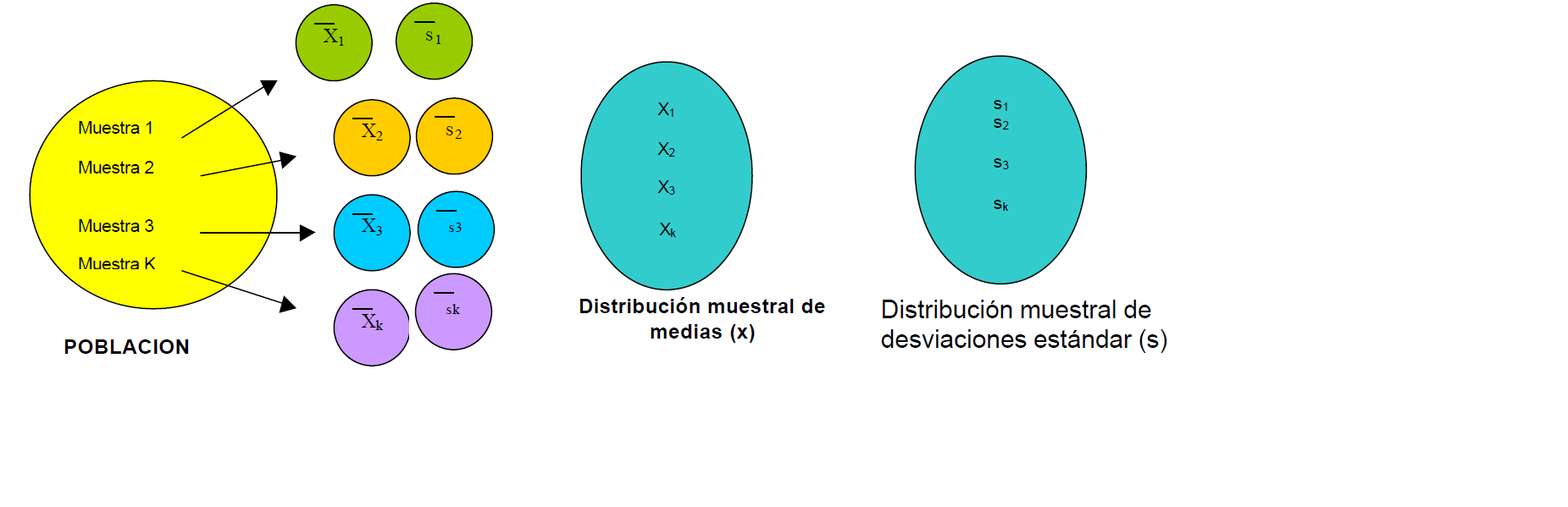
Si la población de la que se extraen las muestras es normal, la distribución muestral de medias será normal sin importar el tamaño de la muestra.
Teorema
Sean \(Y_1, Y_2, . . . , Y_n\) variables aleatorias independientes y distribuidas idénticamente con \(E(Yi)=\mu\) y \(V(Y_i)=\sigma^2 <\infty\).
Entonces: \[\bar Y=\frac{1}{n}\sum_{i=1}^nY_i\]
está distribuida normalmente con media \(\mu_{\bar y }=\mu\) y varianza \(\sigma^2_{\bar y }=\sigma^2/n\)
\[\bar Y \sim N( \mu,\sigma^2/n) \] y la estandarización es:
\[Z=\frac{\bar y-\mu}{\sigma/\sqrt n}\]
Casos de la distribución muestral de medias según la varianza poblacional
1.\(\sigma ^2\) conocida
2.\(\sigma ^2\) desconocida
3.\(\sigma ^2\) desconocida con n>30
| ítem | varianza | Desviación estándar | Estadístico | Distribución |
|---|---|---|---|---|
| Variables aleatorias \(Y_1, Y_2, . . . , Y_n\) | \(\sigma^2\) | \(\sigma\) | \(Z=\frac{y-\mu}{\sigma}\) | \(N(\mu,\sigma^2)\) |
| Distribución muestral \(\bar Y_i\), \(\sigma^2\) conocida | \(\sigma^2_{\bar y }=\sigma^2/n\) | \(\sigma_{\bar y }=\sigma/\sqrt n\) | \(Z=\frac{\bar y-\mu}{S/\sqrt n}\) | \(N(\mu,\sigma^2)\) |
| Distribución muestral \(\bar Y_i\), \(\sigma^2\) desconocida | \(S^2_{\bar y }=S^2/n\) | \(S_{\bar y }=S/\sqrt n\) | \(T=\frac{\bar y-\mu}{S/\sqrt n}\) | \(t_{n-1}\) |
| Distribución muestral \(\bar Y_i\), \(\sigma^2\) desconocida con n>30 | \(\sigma^2_{\bar y }=\sigma^2/n\) | \(\sigma_{\bar y }=\sigma/\sqrt n\) | \(Z=\frac{\bar y-\mu}{S/\sqrt n}\) | \(N(\mu,\sigma^2)\) |
Ejemplo 1
\(\sigma ^2\) desconocida, con n>30
Las calificaciones de exámenes para todos los estudiantes tienen media de 60 y varianza de 64. Una muestra aleatoria de n=100 estudiantes tuvo una calificación media de 58. ¿Hay evidencia para sugerir que el nivel de conocimientos de esta escuela sea inferior?
Solución
Denote con Y la media de una muestra aleatoria de n = 100 calificaciones de una población con \(\mu = 60\) y \(s^2 = 64\).
\[\Large P(\bar Y≤58)\] estandarizamos por medio del teorema de límite central
\[P \left(Z ≤\frac {58-60}{8/\sqrt 100}\right)\] \[\Large P \left (Z ≤\frac {58-60}{0.8} \right)\] \[\Large P \left (z ≤-2.5 \right)=0.0062\]
Ejemplo 2 \(\sigma ^2\) desconocida, con n>30
Los tiempos de servicio para los clientes que pasan por la caja en una tienda de venta al menudeo son variables aleatorias independientes con media de 1.5 minutos y varianza de 1.0.
Calcule la probabilidad de que 100 clientes puedan ser atendidos en menos de 2 horas de tiempo total de servicio.
Solución
Sea \(Y_i\) el tiempo de servicio para el i-ésimo cliente, entonces queremos calcular:
\[\Large P \left( \sum_{i=1}^{100} y_i \leq 120 \right)=\Large P \left( \frac{1}{n}\sum_{i=1}^{100} y_i \leq \frac{120}{n} \right)\] \[P \left(\bar Y \leq \frac{120}{100}\right )=P \left(\bar Y \leq 1.2\right )\]
Como el tamaño muestral es grande, el teorema del límite central nos dice que \(\bar Y\) está distribuida normalmente en forma aproximada con media \(\mu_{\bar y}=\mu=1.5\) y varianza \(\sigma^2_{\bar y=}\sigma^2/n=1/100\)
Por tanto
\[\Large P(\bar Y ≤1.20) = P\left(\frac {\bar Y-\mu}{\sigma/\sqrt n } \leq \frac{1.2-1.5}{1/\sqrt 100}\right )\]
\[\Large P\left(Z \leq \frac{-0.3}{0.1}\right )=P\left(Z \leq -3\right )=0.001\] Entonces, la probabilidad de que 100 clientes puedan ser atendidos en menos de 2 horas es aproximadamente 0.0013. Esta pequeña probabilidad indica que es prácticamente imposible atender a 100 clientes en menos de 2 horas.
Ejemplo 3
Distribución t
Recordemos que en la distribución t \[P(t>b)=\alpha \qquad P(t<b)=\rho\]
\(\sigma ^2\) desconocida Se está realizando un estudio sobre la calidad del aire en una zona. Supongamos que la variable Y: ”Número de medio de microgramos de partículas en suspensión por metro cúbico”, está normalmente distribuida. Se hacen 16 mediciones, en las que se obtiene una cuasidesviación típica de 10.8585 unidades. Obtener la probabilidad de que la media muestral no difiera de la media poblacional en más de 8 unidades.
Solución
El estadístico es una distribución t
\[T=\frac{\bar Y-\mu}{S/\sqrt n}=\frac{\bar Y-\mu}{10.8585/\sqrt 16}=\frac{\bar Y-\mu}{2.7146} \sim t_{n-1}\] \[P(|\bar Y-\mu | \leq 8)=P(\mu - 8 <\bar Y<\mu+8)\]
\[P\left (\frac{\mu-8-\mu}{2.7146}<\frac{\bar Y - \mu}{2.7146} <\frac{+\mu + 8 - \mu}{2.7146}\right)\] \[P(\frac{8}{2.7146}<\frac{\bar Y - \mu}{2.7146} <\frac{8}{2.7146})\] \[P(\frac{8}{2.7146}<t_{15} <\frac{8}{2.7146})\]
Ejercicio propuesto
Una máquina embotelladora puede ser regulada para que descargue un promedio de \(\mu\) onzas por botella. Se ha observado que la cantidad de líquido dosificado por la máquina está distribuida normalmente con \(\sigma= 1.0\) onza. Una muestra de n = 9 botellas se selecciona aleatoriamente de la producción de la máquina en un día determinado (todas embotelladas con el mismo ajuste de la máquina) y las onzas de contenido líquido se miden para cada una.
Determine la probabilidad de que la media muestral se encuentre a no más de 0.3 onza de la verdadera media \(\mu\) para el ajuste seleccionado de la máquina.
¿Cuántas observaciones deben estar incluidas en la muestra si deseamos que Y se encuentre a no más de 0.3 onza de \(\mu\) con probabilidad de 0.95?
Distribución muestral de la varianza
Distribución Chi cuadrado
Un buen estimador de \(\sigma^2\) es la varianza muestral \(S^2\), la distribución asociada a esta distribución es la chi cuadrado.
\[P(\chi^2>\chi^2_\alpha)=\alpha\] \[P(\chi^2 \leq \chi^2_\alpha)=\rho \]
# computing values of 50k random values with 5 degrees of freedom
x <- rchisq(50000, df = 5)
hist(x,
freq = FALSE,
xlim = c(0,16),
ylim = c(0,0.2))
curve(dchisq(x, df = 5), from = 0, to = 15,
n = 5000, col= 'red', lwd=2, add = T)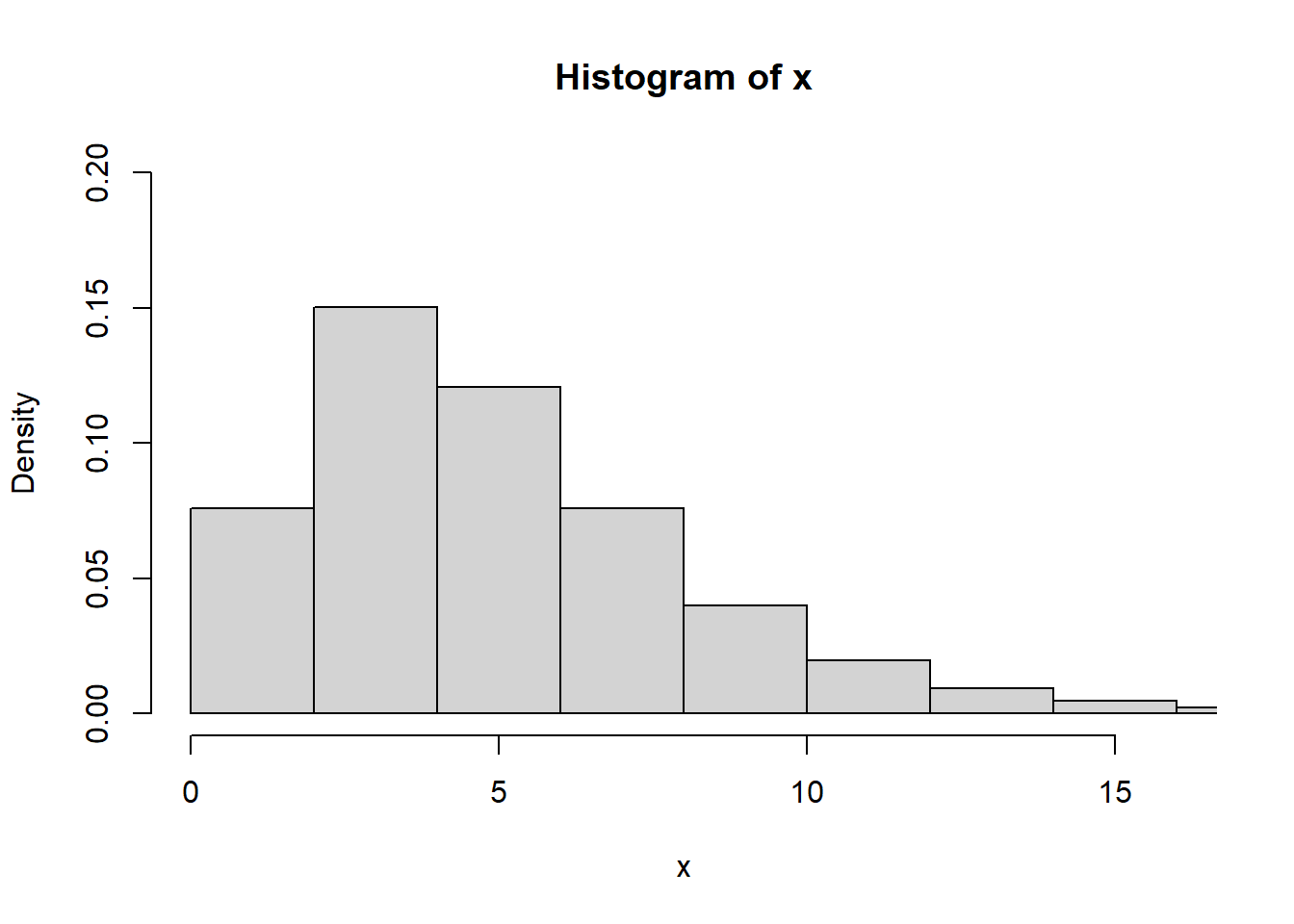
Teorema
Se desea hacer una inferencia acerca de la varianza poblacional basada en una muestra aleatoria \(Y_1, Y_2, . . . , Y_n\) de una población normal, con media \(\mu\) y varianza \(\sigma^2\). Entonces el estadístico corresponde a:
\[\chi^2=\frac{(n-1)S^2}{\sigma^2}=\frac{1}{\sigma^2}\sum_{i=1}^n(Y_i-\bar Y)^2\] tiene una distribución \(\chi^2\) con n-1 grados de libertad. También \(\bar Y\) y \(S^2\) son variables aleatorias independientes.
Para valores grandes de n, la distribución Chi- Cuadrado se aproxima a la distribución Normal. La aproximación se considera aceptable para n > 30
Ejemplo 1
Las onzas de líquido que vierte una máquina embotelladora tienen una distribución normal con \(\sigma^2=1\). Suponga que planeamos seleccionar una muestra aleatoria de diez botellas y medir la cantidad de líquido en cada una. Si estas diez observaciones se usan para calcular \(S^2\). Especifique un intervalo de valores que incluyan \(S^2\) con una probabilidad 0.9. Encuentre números b1 y b2 tales que.
\[P(b_1 \leq S^2 \leq b_2)=0.9\]
Solución
Estandarizar
\[P \left ( \frac{(n-1) b_1}{\sigma^2} \leq \frac{(n-1) S^2}{\sigma^2} \leq \frac{(n-1) b_2 }{\sigma^2}\right)=0.9\] como \(\sigma^2=1\) entonces
\[P\left((n-1) b_1 \leq \chi^2 \leq (n-1) b_2\right)=0.9\]
Podemos usar la Tabla 6 para hallar dos números \(a_1\) y \(a_2\) tales que \[P(a_1 \leq \chi^2\leq a_2)=0.9\]
Se debe encontrar un valor \(a_2\) que delimite un área de 0.05 en la cola superior y el valor de \(a_1\) que delimite 0.05 en la cola inferior (0.95 en la cola superior). Como hay n − 1 = 9 grados de libertad, la Tabla indica que \(a_2=16.919\) y \(a_1 = 3.325\)
# computing values of 50k random values with 5 degrees of freedom
x <- rchisq(50000, df = 9)
hist(x,
freq = FALSE,
xlim = c(0,30),
ylim = c(0,0.2))
curve(dchisq(x, df = 9), from = 0, to = 30,
n = 5000, col= 'red', lwd=2, add = T)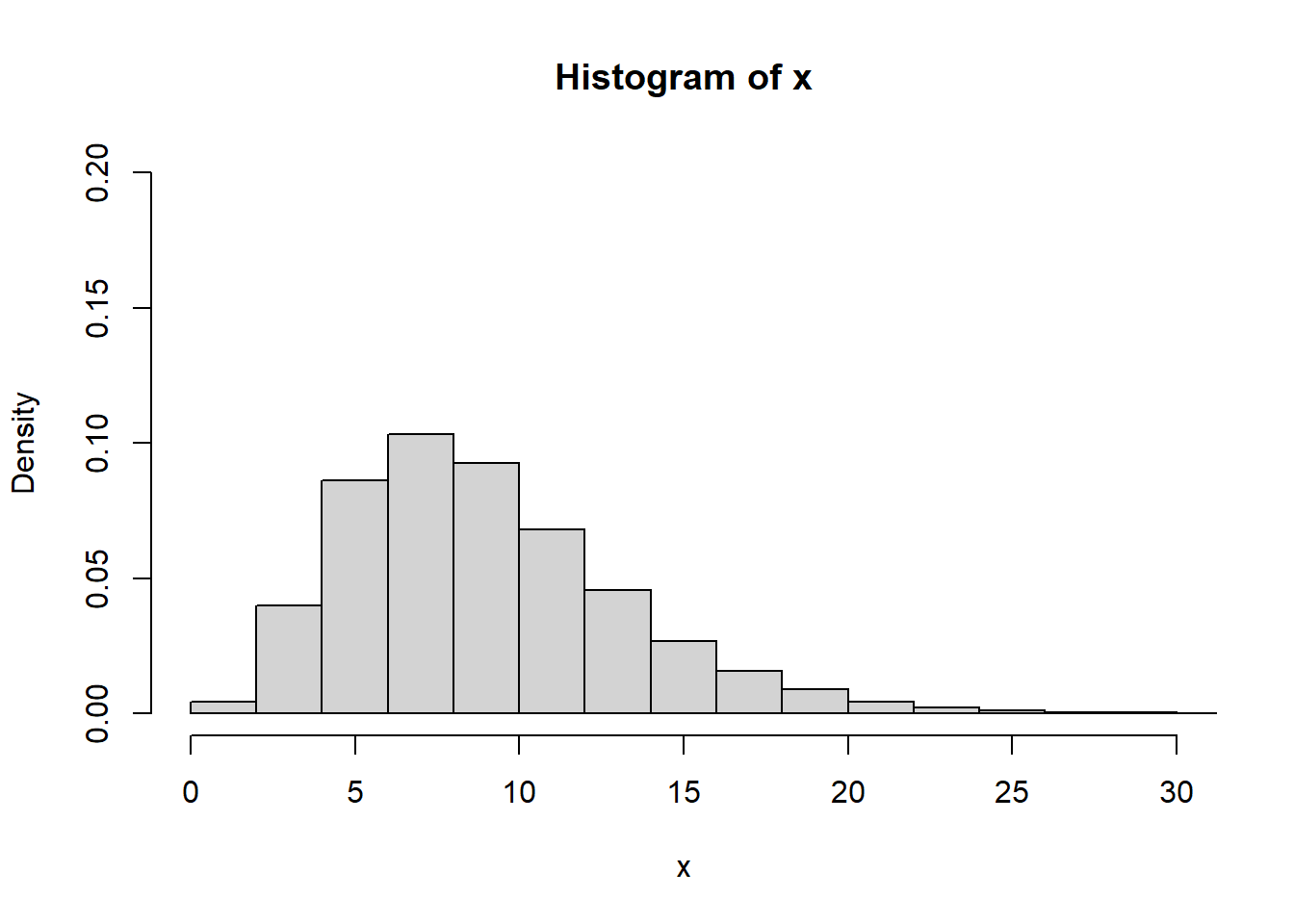
\[16.919=\frac{(n-1) b_2}{\sigma^2}\] \[16.919=\frac{(9) b_2}{\sigma^2}\] como \(\sigma^2=1\) entonces
\[ 16.919 = 9*b_2\] \[b_2=\frac{16.919}{9}\]
encuentre el otro valor b1.
Por tanto, si deseamos tener un intervalo que incluya \(S^2\) con probabilidad 0.90, uno de estos intervalos es (0.369, 1.880).
Ejemplo 2
Se considera una medición física realizada con un instrumento de precisión, donde el interés se centra en la variabilidad de la lectura. Se sabe que la medición es una v.a. con distribución Normal y desviación típica 4 unidades. Se toma una m.a.s. de tamaño 25.Obtener la probabilidad de que el valor de la varianza muestral sea mayor de 12.16 unidades cuadradas
\(X_i\) corresponde las mediciones \(\sim N(\mu;4^2)\) con n=25.
\[\chi^2=\frac{(n-1)S^2}{\sigma^2}\] \[P(S^2\geq 12.16)\] Estandarizamos. \[P \left (\frac{(n-1)S^2}{\sigma^2}\geq \frac{(24)*12.16}{16} \right )\]
\[P \left (\chi^2\geq 18.24 \right )=79.12 \%\]
#lower.tail=FALSE
#cola derecha P(x>alfa)
pchisq(18.24, df=24, lower.tail=FALSE)## [1] 0.7912132Distribución muestral de Proporciones
Se desea investigar la proporción de artículos defectuosos. Esta distribución se genera extrayendo muestras de la población y calculando la proporción (p=x/n en donde “x” es el número de éxitos u observaciones de interés y “n” el tamaño de la muestra).
La fórmula que se utilizará para el cálculo de probabilidad en una distribución muestral de proporciones está basada en la aproximación de la distribución normal a la binomial. Esta fórmula nos servirá para calcular la probabilidad del comportamiento de la proporción en la muestra.
\[z=\frac{\hat p-P}{\sqrt{\frac{Pq}{n}}}\]
Ejemplo: Se ha determinado que 60% de los estudiantes de una universidad grande fuman cigarrillos. Se toma una muestra aleatoria de 800 estudiantes. Calcule la probabilidad de que la proporción de la muestra de la gente que fuma cigarrillos sea menor que 0.55.
Ejemplo
n=800 est P=0.6 p=0.55
\[P(\hat p<0.55)\]
Aplicando factor de corrección por continuidad (0.5/n)
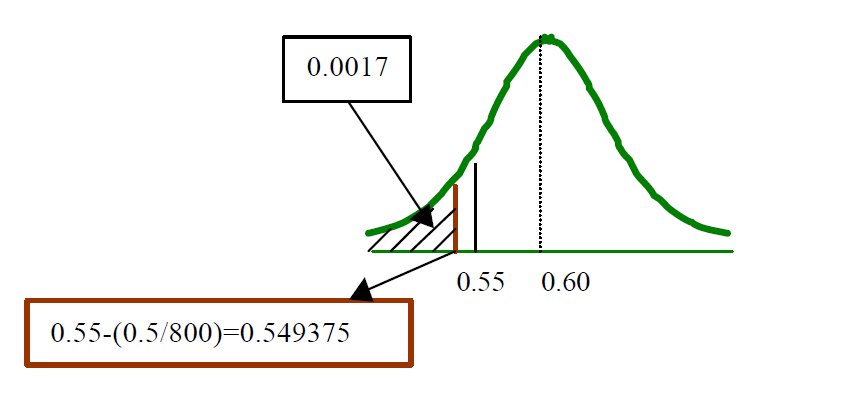
\[P(\hat p\leq 0.5493)=P\left(\frac{\hat p-P}{\sqrt{\frac{Pq}{n}}}\leq\frac{0.5493-0.6}{\sqrt{\frac{0.6*0.4}{800}}}\right)=-2.92\] \[P\left(z\leq -2.92 \right)=0.0018\] Ejercicio 2
El gerente de Mcdonald cree que el 30% de los clientes son nuevos. Para comprobar esta afirmación se toma una muestra aleatoria de 100 clientes.
- Suponga que el presidente está en lo correcto y que p=0.30. ¿Cuál es la distribución muestral de p para este estudio?
\[P\sim N(P,\frac{Pq}{n})\] P=0.3 n=100 \[P\sim N(0.3,0.021)\]
- ¿Cuál es la probabilidad de que la proporción muestral esté a mas o menos 0.05 de la proporción poblacional
\[P \left (P-0.05\leq \hat P \leq P+0.05\right )\] \[P \left ( P \leq P+0.05\right)- P \left ( P \leq P-0.05\right)\] Aplicando factor de corrección
\[P \left ( P \leq P+0.05+(0.5/n)\right)- P \left ( P \leq P-0.05-(0.5/n)\right)\] \[P \left ( P \leq P+0.05+0.005\right)- P \left ( P \leq P-0.05-0.005)\right)\]
Estandarizando
\[P \left ( \hat P \leq P+0.055\right)- P \left ( \hat P \leq P-0.055\right)\]
\[P \left (\frac{\hat P-P}{\sqrt{\frac{Pq}{n}}} \leq \frac{P+0.055-P}{\sqrt{\frac{Pq}{n}}}\right)- P \left ( \frac{\hat P-P}{\sqrt{\frac{Pq}{n}}} \leq \frac{P-0.055-P}{\sqrt{\frac{Pq}{n}}}\right)\] \[ P \left (z \leq \frac{P+0.055-P}{\sqrt{\frac{0.3*0.7}{100}}}\right)- P \left ( z \leq \frac{P-0.055-P}{\sqrt{\frac{0.3*0.7}{100}}}\right)\] \[ P \left (z \leq \frac{0.055}{0.046}\right)- P \left ( z \leq \frac{-0.055}{0.046}\right)\] \[ P \left (z \leq 1.19\right)- P \left ( z \leq \frac{-0.055}{0.046}\right)\]
- ¿Cuál es la probabilidad de que la proporción muestral sea mas de 0.4?
Distribuciones muestrales para dos muestras
Distribución de la diferencia de medias muestrales
1. Varianzas poblacionales conocidas
\[(\bar X - \bar Y) \sim N \left ( (\mu_x-\mu_y), \frac{\sigma^2_x}{n_x}+\frac{\sigma^2_y}{n_y}\right) \]
El estadístico es:
\[Z=\frac{(\bar X - \bar Y)-(\mu_x-\mu_y)}{\sqrt{\frac{\sigma^2_x}{n_x}+\frac{\sigma^2_y}{n_y}}} \longrightarrow N(0,1)\] Ejemplo
Los niveles de radiación latente en dos regiones A y B siguen distribuciones Normales independientes de medias 0.48 y 0.46 y varianzas 0.2 y 0.01 rem por año, respectivamente. Se realizan 25 mediciones en la región A y 100 en la B.
X: “Nivel radiación latente en A”
Y: “Nivel radiación latente en B”
| Regiones | media | var | n |
|---|---|---|---|
| A | 0.48 | 0.2 | 25 |
| B | 0.46 | 0.01 | 100 |
| A-B | 0.02 |
Obtener la probabilidad de que la media de la muestra A sea como máximo 0.2 rem superior a la media de la muestra B.
\[P(\bar X_A \leq \bar Y_B+0.2) \]
\[P(\bar X - \bar Y \leq 0.2) \]
2. Varianzas poblacionales desconocidas pero iguales
La condición de igualdad de varianzas debe comprobarse o afirmarse.
\[\sigma^2_x=\sigma^2_y\]
\[(\bar X - \bar Y) \sim t_{n_x,n_y,2} \]
\[\mu= (\mu_x-\mu_y)\] \[var=S_p^2 \left (\frac{1}{n_x}+\frac{1}{n_y} \right )\]
El estadístico es:
\[T=\frac{(\bar X - \bar Y)-(\mu_x-\mu_y)}{S_p\sqrt{\frac{1}{n_x}+\frac{1}{n_y}}} \longrightarrow t_{(n_x,n_y,2)}\] Donde: \[S^2_p=\frac{(n_x-1)S^2_x+(n_y-1)S^2_y}{n_x+n_y-2}\]
Tiene una distribución t de student con \(n_x+n_y-2\)
Ejemplo
Se está realizando un estudio sobre la calidad del aire en dos zonas A y B. Un indicador de la calidad es el número de microgr de partículas en suspensión por \(m^3\) de aire, que suponemos siguen distribuciones Normales independientes de media 62.237 en A, 61.022 en B y varianzas iguales. En la zona A se realizan 12 mediciones, obteniéndose una varianza de 8.44 microgr2 y en la B 15 mediciones, con una varianza de 9.44 microgr2.
| Zona | media | var | n |
|---|---|---|---|
| A | 62.24 | 8.44 | 12 |
| B | 61.02 | 9.44 | 15 |
| A-B | 1.22 |
Obtener la probabilidad de que la media muestral de A sea como mínimo tres unidades superior a la media muestral de B.
\[P(\bar X_A \geq3+\bar Y_b) \]
pt(1.53, 25, lower.tail = F)## [1] 0.069286523. Varianzas poblacionales desconocidas o no con tamaños de muestra \(n_1>30\) y \(n_2>30\)
\[(\bar X - \bar Y) \sim N \left ( (\mu_x-\mu_y), \frac{S^2_x}{n_x}+\frac{S^2_y}{n_y}\right) \] El estadístico es:
\[Z=\frac{(\bar X - \bar Y)-(\mu_x-\mu_y)}{\sqrt{\frac{S^2_x}{n_x}+\frac{S^2_y}{n_y}}} \longrightarrow N(0,1)\]
4. Varianzas poblacionales desconocidas y diferentes
El estadístico es:
\[T=\frac{(\bar X - \bar Y)-(\mu_x-\mu_y)}{\sqrt{\frac{S^2_x}{n_x}+\frac{S^2_y}{n_y}}} \longrightarrow t_g\] los grados de libertad están dados por:
\[g=\frac{\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\frac{\left(\frac{s_1^2}{n_1}\right)^2}{n_1+1}+\frac{\left(\frac{s_2^2}{n_2}\right)^2}{n_2+1}}-2\]
Distribución de la diferencia de proporciones muestrales
\[\hat P_X - \hat P_Y \sim N \left ( P_x-P_y, \frac{P_xq_x}{n_x}+\frac{P_yq_y}{n_y}\right) \]
El estadístico es:
\[Z=\frac{(\hat P_X -\hat P_y)-(P_x-P_y)} {\sqrt{\frac{P_xq_x}{n_x}+\frac{P_yq_y}{n_y}}} \longrightarrow N(0,1)\] Ejemplo
Se sabe que en una población el 28% de las mujeres y el 25% de los hombres son fumadores. Se extraen muestras de 42 mujeres y 40 hombres. Determinar la probabilidad de que las mujeres fumadoras superen a los hombres fumadores en al menos el 4%.
\(p_M:\) Proporción de mujeres fumadoras en la población 0.28
\(p_H:\) Proporción de mujeres fumadoras en la población 0.25
\(\hat p_M:\) Proporción de mujeres fumadoras en la muestra
\(\hat p_H\)“Proporción de mujeres fumadoras en la muestra
| Genero | P | q | n |
|---|---|---|---|
| Mujer | 0.28 | 0.72 | 42 |
| Hombre | 0.25 | 0.75 | 40 |
| Dif | 0.03 |
la pregunta es:
\[P(\hat p_M \geq \hat p_H+0.04)\] \[P(\hat p_M -\hat p_H\geq 0.04)\]
Distribución del cociente de varianzas muestrales de dos poblaciones Normales independientes
Distribución F
El estadístico F, definido como:
\[F=\frac{S^2_x*\sigma_y^2}{S^2_y*\sigma_x^2} \longrightarrow F_{n_x-1,n_y-1}\] Ejemplo
Se está comparando la variabilidad de los índice de biodiversidad (I.B.D) de dos ríos A y B, que suponemos siguen distribuciones Normales. Se realizan 16 mediciones en el río A y se obtiene una varianza de 9.52, y 18 mediciones en el río B y se obtiene una varianza de 7.
X: “I.B-D en el río A
Y: “I.B-D en el río B
| Rio | var | n |
|---|---|---|
| A | 9.52 | 16 |
| B | 7 | 18 |
Obtener la probabilidad de que la varianza en el río B sea como mínimo el doble de la varianza en el río A.
\[P(S^2_B\geq 2*S^2_A)\]
\[P\left ( \frac{S^2_B}{S ^2_A}\geq 2 \right)\] Estandarizando
\[P \left ( \frac{S^2_B\sigma^2_A}{S^2_A\sigma^2_B}\geq 2 \frac{S^2_A}{S^2_B}\right )\]
\[P \left ( F_{15,17}\geq 2 *\frac{9.57}{7}\right )\] \[P \left ( F_{15,17}\geq 2.73 \right )\]
pf(q=2.73, df1=15,df2=17, lower.tail=FALSE)## [1] 0.02471903